

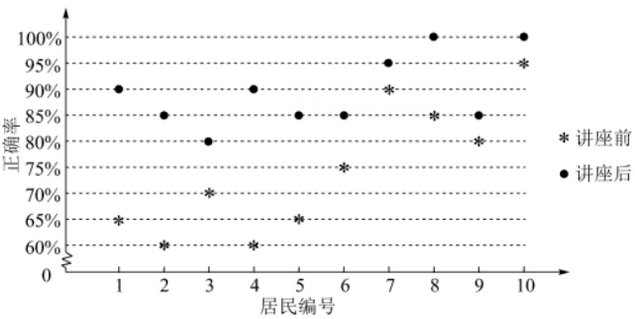
则( )

由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
|
试验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
伸缩率 |
545 |
533 |
551 |
522 |
575 |
544 |
541 |
568 |
596 |
548 |
|
伸缩率 |
536 |
527 |
543 |
530 |
560 |
533 |
522 |
550 |
576 |
536 |
记 , 记
的样本平均数为
, 样本方差为
.
| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
| 根部横截面积 | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
| 材积量 | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
并计算得 .
附:相关系数 .
对照组的小白鼠体重的增加量从小到大排序为
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
试验组的小白鼠体重的增加量从小到大排序为
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
|
|
|
|
|
对照组 |
||
|
试验组 |
(ⅱ)根据(i)中的列联表,能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
附: ,
|
|
0.100 |
0.050 |
0.010 |
|
|
2.706 |
3.841 |
6.635 |
|
试验序号i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
伸缩率 |
545 |
533 |
551 |
522 |
575 |
544 |
541 |
568 |
596 |
548 |
|
伸缩率 |
536 |
527 |
543 |
530 |
560 |
533 |
522 |
550 |
576 |
536 |
记 , 记
,
, …,
的样本平均数为
, 样本方差为
,

利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳形,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为
.假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.
|
一级品 |
二级品 |
合计 |
|
|
甲机床 |
150 |
50 |
200 |
|
乙机床 |
120 |
80 |
200 |
|
合计 |
270 |
130 |
400 |
附:
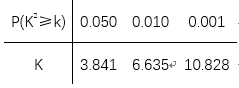
|
旧设备 |
9.8 |
10.3 |
10.0 |
10.2 |
9.9 |
9.8 |
10.0 |
10.1 |
10.2 |
9.7 |
|
新设备 |
10.1 |
10.4 |
10.1 |
10.0 |
10.1 |
10.3 |
10.6 |
10.5 |
10.4 |
10.5 |
旧设备和新设备生产产品的该项指标的样本平均数分别记为 和
,样本方差分别记为s12和s22
附:相关系数r= ,
=1.414.
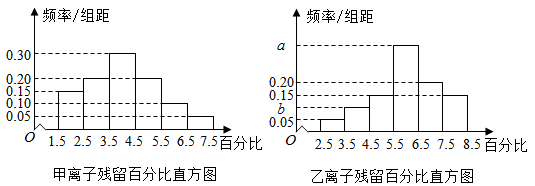
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
| y的分组 | [-0.20,0) | [0,0.20) | [0.20,0.40) | [0.40,0.60) | [0.60,0.80) |
| 企业数 | 2 | 24 | 53 | 14 | 7 |
附: