
 B .
B . 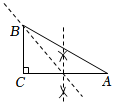 C .
C .  D .
D . 
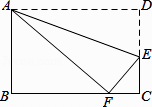


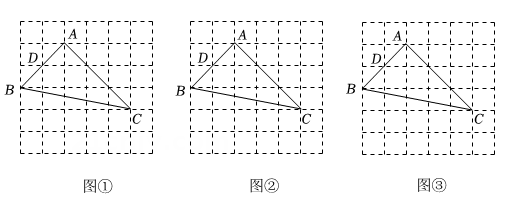
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 , 拱顶离水面
. 据调查,该河段水位在此基础上再涨
达到最高.

素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂长的灯笼,如图3.为了安全,灯笼底部距离水面不小于
;为了实效,相邻两盏灯笼悬挂点的水平间距均为
;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.

[温故知新]
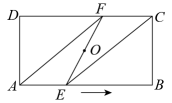
在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作CF∥AD交DE的延长线于点F,再证△ADE≌△CFE,再证四边形DBCF是平行四边形,即可证明定理.
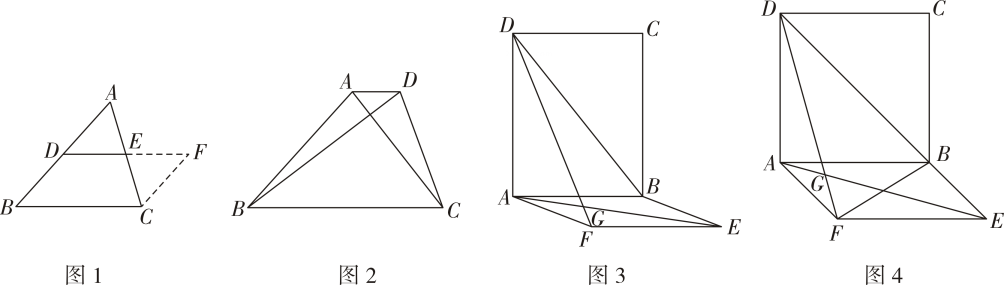
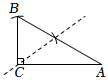
小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形ABCD中,AD∥BC,AC⊥BD,若AC=3,BD=4,AD=1,则BC的值为
如图3,在矩形ABCD和ABEF中,连接DF、AE交于点G,连接DB.若AE=DF=DB,求∠FGE的度数;
如图4在第(2)题的条件下,连接BF,若AB=4D= , 求△BEF的面积.