备考2024年浙江中考数学一轮复习专题21.2四边形真题模...

更新时间：2024-03-02 浏览次数：50 类型：一轮复习

一、选择题（每题3分，共30分）

1. 下列命题正确的是（）

A . 对角线相等的四边形是平行四边形 B . 对角线相等的四边形是矩形 C . 对角线互相垂直的平行四边形是菱形 D . 对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
2. (2023八上·武鸣期中) 已知正多边形的一个外角等于40°，那么这个正多边形的边数为（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
3. (2019九上·海宁月考) 用四个全等的直角三角形无空隙、无重叠地拼成一个菱形，该菱形的边长的平方等于两条对角线的积，则这四个直角三角形的最小内角是（）

A . 60° B . 45° C . 30° D . 15°

答案解析收藏纠错 + 选题
4. (2023九上·滕州月考) 如图，在菱形ABCD中，AB=1，∠DAB=60°，则AC的长为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·湖州) 如图，已知∠AOB ，以点O为圆心，适当长为半径作圆弧，与角的两边分别交于C ， D两点，分别以点C ， D为圆心，大于 $\text{[math]}$ 长为半径作圆弧，两条圆弧交于∠AOB内一点P ，连结OP ，过点P作直线PE∥OA ，交OB于点E ，过点P作直线PF∥OB ，交OA于点F ．若∠AOB＝60°，OP＝6cm ，则四边形PFOE的面积是（　　）

A . $\text{[math]}$ cm² B . $\text{[math]}$ cm² C . $\text{[math]}$ cm² D . $\text{[math]}$ cm²

答案解析收藏纠错 + 选题
6. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 为对角线 $\text{[math]}$ 的中点， $\text{[math]}$ .动点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，动点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 同时从点 $\text{[math]}$ 出发，分别向终点 $\text{[math]}$ 运动，且始终保持 $\text{[math]}$ .点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ ；点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ .在整个过程中，四边形 $\text{[math]}$ 形状的变化依次是（）

A . 菱形→平行四边形→矩形→平行四边形→菱形 B . 菱形→正方形→平行四边形→菱形→平行四边形 C . 平行四边形→矩形→平行四边形→菱形→平行四边形 D . 平行四边形→菱形→正方形→平行四边形→菱形

答案解析收藏纠错 + 选题
7. (2024·新乐模拟) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ，边 $\text{[math]}$ 上的动点．下列四种说法：
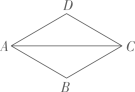
①存在无数个平行四边形 $\text{[math]}$ ；
②存在无数个矩形 $\text{[math]}$ ；
③存在无数个菱形 $\text{[math]}$ ；
④存在无数个正方形 $\text{[math]}$ ．其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2023九上·宝安月考) 如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤AM= $\text{[math]}$ MF.其中正确结论的是（）

A . ①③④ B . ②④⑤ C . ①③④⑤ D . ①③⑤

答案解析收藏纠错 + 选题
9. (2023九上·新昌期中) 如图，四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连结EG，BD相交于点O，BD与HC相交于点P.若 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ .正确的是（）

A . ②③④ B . ①③④ C . ①②④ D . ①②③

答案解析收藏纠错 + 选题
10. 如图，已知矩形纸片ABCD，其中 $\text{[math]}$ ，现将纸片进行如下操作：
第一步，如图①将纸片对折，使AB与DC重合，折痕为EF，展开后如图②；

第二步，再将图②中的纸片沿对角线BD折叠，展开后如图③；

第三步，将图③中的纸片沿过点E的直线折叠，使点C落在对角线BD上的点H处，如图④．
则DH的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2023·台州) 如图，矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ．在边AD上取一点E，使 $\text{[math]}$ ，过点C作 $\text{[math]}$ ，垂足为点F，则BF的长为．

答案解析收藏纠错 + 选题
12. (2023·杭州模拟) 如图，正六边形ABCDEF的边长为2cm，点P是线段BF上一点，则阴影部分的面积为cm²

答案解析收藏纠错 + 选题
13. (2023九上·苍南模拟) 如图，矩形ABCD中，AB=1，BC=2，AE为∠BAD的平分线，F为AE上一动点，点M为DF的中点，连接BM，则BM的最小值是.

答案解析收藏纠错 + 选题
14. 如图，在菱形 ABCD中，∠A=60° ，AB=6．折叠该菱形，使点A落在边BC上的点M 处，折痕分别与边 AB，AD交于点E，F．当点M与点B重合时，EF的长为；当点M的位置变化时，DF长的最大值为．

答案解析收藏纠错 + 选题
15. (2023·杭州模拟) 如图，在矩形ABCD中，点E是AD的中点，连接BE ，将△ABE沿着BE翻折得到△FBE ， EF交BC于点H ，延长BF ， DC相交于点G ，若DG＝8，BC＝12，则AB＝，EH＝．

答案解析收藏纠错 + 选题
16. (2024九下·淳安期中) 如图，标号为①，②，③，④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD ，相邻图形之间互不重叠也无缝隙，①和②分别是等腰Rt△ABE和等腰Rt△BCF ， ③和④分别是Rt△CDG和Rt△DAH ， ⑤是正方形EFGH ，直角顶点E ， F ， G ， H分别在边BF ， CG ， DH ， AE上．
1. （1）若EF＝3cm ， AE+FC＝11cm ，则BE的长是 cm ．
2. （2）若 $\text{[math]}$ ，则tan∠DAH的值是．
答案解析收藏纠错 + 选题

三、作图题（共6分）

17. (2024九下·丰城期中) 分别在图①、图②中按要求作图（保留作图痕迹，不写作法）．
1. （1）如图①，在 $\text{[math]}$ 的方格纸中，点 $\text{[math]}$ 都在格点上，在图①中找一个格点D，使以点 $\text{[math]}$ 为顶点的四边形是平行四边形；
2. （2）如图②，已知四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 为对角线，点P为 $\text{[math]}$ 上任意一点，请仅用无刻度的直尺在 $\text{[math]}$ 上找出另一点Q，使 $\text{[math]}$ ．
答案解析收藏纠错 + 选题

四、解答题（共5题，共38分）

18. (2024·武汉模拟) 小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD.求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．

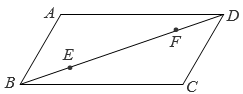
小惠：

证明：∵AC⊥BD，OB＝OD，

∴AC垂直平分BD．

∴AB＝AD，CB＝CD，

∴四边形ABCD是菱形．

小洁：

这个题目还缺少条件，需要补充一个条件才能证明．

若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．

答案解析收藏纠错 + 选题

19. (2021九上·余姚期中) 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD ．

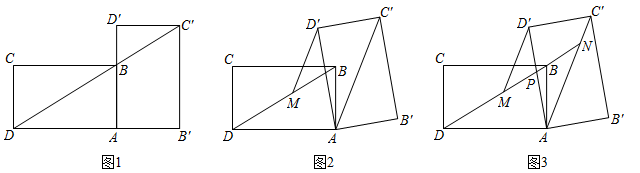
[探究1]如图1，当α＝90°时，点C′恰好在DB延长线上．若AB＝1，求BC的长．

[探究2]如图2，连结AC′，过点D′作D′M∥AC′交BD于点M ．线段D′M与DM相等吗？请说明理由．

[探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P ， N（如图3），发现线段DN ， MN ， PN存在一定的数量关系，请写出这个关系式，并加以证明．

答案解析收藏纠错 + 选题
20. (2023·杭州模拟) 正方形ABCD的边长为1，连接BD ，过点C作BD的平行线CE ， BE与CD相交于点F ，过点D作DH⊥BE ．
1. （1）求△BDE的面积；
2. （2）当∠CBE＝15°时，求BE的长；
3. （3）若△EFC的面积记为S₁ ， △DFH的面积记为S₂ ， △DBF的面积记为S₃ ， △BFC的面积记为S₄ ， $\text{[math]}$ ，请用k的代数式表示 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2023·衢州) 如图1，点 $\text{[math]}$ 为矩形ABCD的对称中心， $\text{[math]}$ ，点 $\text{[math]}$ 为AD边上一点 $\text{[math]}$ ，连结EO并延长，交BC于点 $\text{[math]}$ .四边形ABFE与 $\text{[math]}$ 关于EF所在直线成轴对称，线段 $\text{[math]}$ 交AD边于点 $\text{[math]}$ 。
1. （1）求证： $\text{[math]}$ .
2. （2）当 $\text{[math]}$ 时，求AE的长.
3. （3）令AE=a，DG=b.
  ①求证：(4-a)(4-b)=4.
  
  ②如图2，连结 $\text{[math]}$ ，分别交 $\text{[math]}$ 于点H，K.记四边形OKGH的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ .当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2023九上·义乌月考) 如图，在矩形ABCD中，AD＝2 $\text{[math]}$ ，AB＝4 $\text{[math]}$ ，DM⊥AC于点M ，在对角线AC上取一点N ，使得2CN＝3AM ，连接DN并延长交BC于点E ， F是AB上一点，连接EF ， MF ．当点P从点E匀速运动到点F时，点Q恰好从点M匀速运动到点N ．
1. （1）求AM ， CE的长．
2. （2）若EF∥AC ，记EP＝x ， AQ＝y ．
  ①求y关于x的函数表达式．
  
  ②连接PQ ，当直线PQ平行于四边形DEFM的一边时，求所有满足条件的x的值．
3. （3）在运动过程中，当直线PQ同时经过点B和D时，记点Q的运动速度为v₁ ，记点P的运动速度为v₂ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

五、实践探究题（共3题，共28分）

23. (2023·湖州)
1. （1）【特例感知】
  如图1，在正方形ABCD中，点P在边AB的延长线上，连结PD ，过点D作DM⊥PD ，交BC的延长线于点M ．求证：△DAP≌△DCM ．
2. （2）【变式求异】
  如图2，在Rt△ABC中，∠ABC＝90°，点D在边AB上，过点D作DQ⊥AB ，交AC于点Q ，点P在边AB的延长线上，连结PQ ，过点Q作QM⊥PQ ，交射线BC于点M ．已知BC＝8，AC＝10，AD＝2DB ，求 $\text{[math]}$ 的值．
3. （3）【拓展应用】
  如图3，在Rt△ABC中，∠BAC＝90°，点P在边AB的延长线上，点Q在边AC上（不与点A ， C重合），连结PQ ，以Q为顶点作∠PQM＝∠PBC ， ∠PQM的边QM交射线BC于点M ．若AC＝mAB ， CQ＝nAC（m ， n是常数），求 $\text{[math]}$ 的值（用含m ， n的代数式表示）．
答案解析收藏纠错 + 选题
24. (2022·衢州模拟) 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD.
1. （1） [探究1]如图1，当α＝90°时，点C′恰好在DB延长线上.若AB＝1，求BC的长.
2. （2） [探究2]如图2，连结AC′，过点D′作 $\text{[math]}$ 交BD于点M，线段D′M与DM相等吗？请说明理由.
3. （3） [探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P，N（如图3），发现线段DN，MN，PN存在一定的数量关系，请写出这个关系式，并加以证明.
答案解析收藏纠错 + 选题
25. (2021九上·清远期末) 如图，
1. （1）【推理】
  如图1，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G.
  求证： $\text{[math]}$ .
2. （2）【运用】
  如图2，在（推理）条件下，延长BF交AD于点H.若 $\text{[math]}$ ， $\text{[math]}$ ，求线段DE的长.
3. （3）【拓展】
  将正方形改成矩形，同样沿着BE折叠，连结CF，延长CF，BF交直线AD于G，两点，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值（用含k的代数式表示）.
答案解析收藏纠错 + 选题