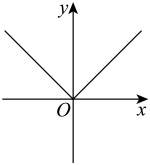
 B .
B . 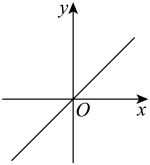 C .
C .  D .
D . 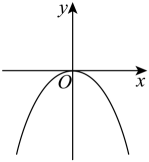
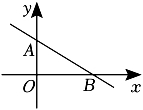
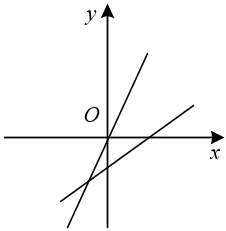 B .
B . 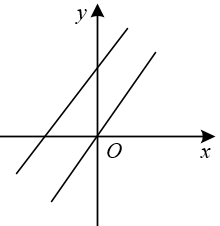 C .
C . 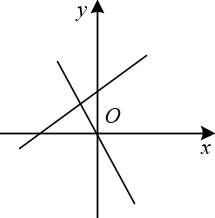 D .
D . 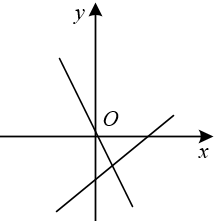

【阅读感悟】
在平面直角坐标系中,已知点 , 当t的值发生改变时,点Q的位置也会发生改变,为了求点Q运动所形成的图象的解析式,令点Q的横坐标x , 纵坐标y , 得到了方程组
消去t , 得
, 即
, 可以发现,点
随t的变化而运动所形成的图象的解析式是
.
观察下列四个点的坐标,不在函数图象上的是____.
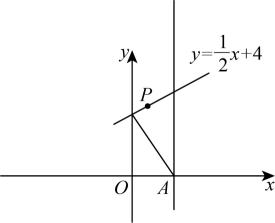
如图,在平面直角坐标系中,点P在一次函数的图象上运动.已知点
为定点,连接
, 过点A作直线
, 且
, 求点B随点P的变化而运动所形成的图象的解析式.
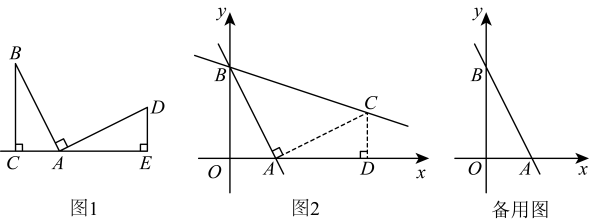
如图 ,
,
, 过点
作
于点
, 过点
作
于点
. 则
. 我们把这个数学模型称为“
字”模型或“一线三等角”模型.
【模型应用】
在平面直角坐标系中,直线与
轴交于点
, 与
轴交于点
.
小明想利用“一线三等角”模型解决这个问题.如图,过点作
的垂线交
于点
, 再过点
作
轴的垂线,垂足为
, 可求出点
的坐标为,从而求得直线
的表达式为.
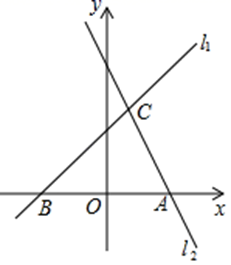
①若点D为直线上一点,若
, 求点D的坐标;
②过点O作直线 , 若点M、N分别是直线
和
上的点,且满足
. 请问是否存在这样的点
, 使得
为直角三角形?若存在,请求出点N的坐标;若不存在,请说明理由.