
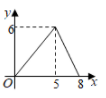
 B .
B . 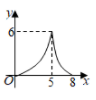 C .
C . 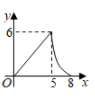 D .
D . 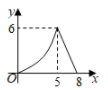


 B .
B . 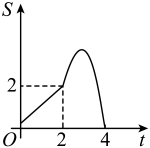 C .
C .  D .
D . 



|
时间x秒 |
… |
2 |
4 |
6 |
… |
|
面积ycm2 |
… |
12 |
|
|
… |
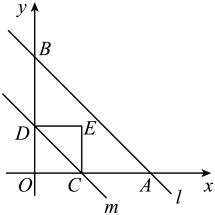
①当时,求线段
的长;
②若点M,N,E三点中,其中两点恰好关于第三点对称,直接写出此时m的值.


①当时,试探究
与t之间的函数关系式.
②在直线m的运动过程中,当t为何值时,为
面积的
?
①当时,求
的面积
②当点P , Q运动至四边形为矩形时,请求出此时t的值.

若
的面积为
, 求点
的坐标;
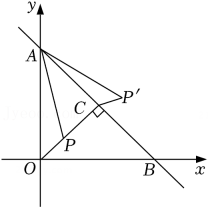
如图
, 当点
在
轴正半轴上时,将直线
绕点
逆时针旋转
后的直线与线段
交于点
, 连接
, 若
, 求线段
的长.


材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:
在直线l1:y=k1x+b1与直线l2:y=k2x+b2中,如果k1=k2且b1≠b2 , 那么l1∥l2 , 反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:
在直线l1:y=k1x+b1与l2:y=k2x+b2中,如果k1•k2=﹣1,那么l1⊥l2 , 反过来,也成立
应用举例
已知直线y=﹣ x+5与直线y=kx+2互相垂直,则﹣
k=﹣1.所以k=6
解决问题

①在平面直角坐标系中,点P是原点O的“正方形关联点”.若
, 则O、P的“关联正方形”的周长是 ▲ ;若点P在直线
上,则O、P的“关联正方形”面积的最小值是 ▲ .
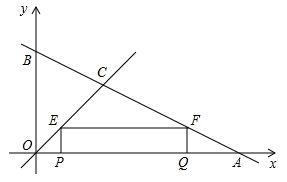
②如图2,已知点 , 点B在直线
上,正方形
是A、B的“关联正方形”,顶点P、Q到直线l的距离分别记为a和b,求
的最小值.