2024年人教版中考数学二轮复习专题18 图形的旋转、平移...

更新时间：2024-04-17 浏览次数：34 类型：二轮复习

一、单选题

1. (2023九上·禄劝期中) 如图，将 $\text{[math]}$ 绕顶点A逆时针旋转70°，得到 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 22° B . 24° C . 35° D . 46°

答案解析收藏纠错 + 选题
2. (2023七下·武昌期中) 如图，已知 $\text{[math]}$ ，点E，F分别在直线 $\text{[math]}$ 上，点P在 $\text{[math]}$ 之间且在 $\text{[math]}$ 的左侧.若将射线 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，射线 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，折叠后的两条射线互相垂直，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九下·杭州月考) 如图，在四边形纸片ABCD中，AD∥BC ， AB＝10，∠B＝60°，将纸片折叠，使点B落在AD边上的点G处，折痕为EF ，若∠BFE＝45°，则BF的长为（）

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·海曙模拟) 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到，点C在边EF上，过点E作AD平行线得矩形ANMD，则要知道矩形ANMD的面积只需知道（）

A . S_△_BEC B . S_△B_GC C . S_△E_CM D . S_△C_GF

答案解析收藏纠错 + 选题
5. (2023八下·安源期中) 如图，将 $\text{[math]}$ 沿 $\text{[math]}$ 方向平移得到 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·简阳月考) 下列命题是真命题的是（）

A . 平行四边形的对角线相等 B . 经过旋转，对应线段平行且相等 C . 两组对角分别相等的四边形是平行四边形 D . 两边相等的两个直角三角形全等

答案解析收藏纠错 + 选题
7. (2023·邗江模拟) 如图，在菱形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， E是 $\text{[math]}$ 边的中点，将菱形纸片沿过点A的直线折叠，使点B落在直线 $\text{[math]}$ 上的点G处，折痕为 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点H，有如下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，上述结论中，所有正确结论的序号是（）

A . ①②④ B . ①②③ C . ①③④ D . ①②③④

答案解析收藏纠错 + 选题
8. (2023八上·田家庵期中) 如图，四边形ABCD中，AB=AD，点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点B′恰好落在CD上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八上·温州期中) 如图，在△ABC中，∠BAC=90°，AB=AC=3，D，E分别在边AB，AC上，且DE∥BC，将△ABC沿DE翻折，点A的对应点为A'，A'D和A'E分别交BC于G，F，若A'F=1，则四边形DEFG的面积为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
10. 如图，已知长方形纸片 ABCD，点E，F分别在边AD和BC上，且∠EFC=53°，H和G 分别是边AD和 BC 上的动点，现将点 A，B 沿 EF 向下折叠至点N，M 处，将点 C，D沿GH 向上折叠至点P，K 处，若 MN∥PK，则∠KHD的度数为（）

A . 37°或143° B . 74°或96° C . 37°或105° D . 74°或106°

答案解析收藏纠错 + 选题

二、填空题

11. (2023·静安模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕着点 $\text{[math]}$ 旋转后，点 $\text{[math]}$ 落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的大小是．

答案解析收藏纠错 + 选题
12. (2023九下·义乌月考) 如图，四边形 $\text{[math]}$ 是边长为5的正方形，E是 $\text{[math]}$ 上一点， $\text{[math]}$ ，将 $\text{[math]}$ 绕着点A顺时针旋转到与 $\text{[math]}$ 重合，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024九下·新余开学考) 如图，一副三角板的三个内角分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，如图，若固定 $\text{[math]}$ ，将 $\text{[math]}$ 绕着公共顶点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 度（ $\text{[math]}$ ），当边 $\text{[math]}$ 与 $\text{[math]}$ 的某一边平行时，相应的旋转角 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2023八下·拱墅期末) 如图是一张矩形纸片ABCD，点E在边BC上，且满足 AB＝2BE，把△ABE沿直线AE折叠，使点B落在点F处，EF的延长线与边CD交于点G．若CG＝DG，则 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
15. 如图， $\text{[math]}$ 的半径为2 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的弦，点C为 $\text{[math]}$ 上的一点，将 $\text{[math]}$ 沿弦 $\text{[math]}$ 翻折，使点C与圆心O重合，则阴影部分的面积为.（结果保留π与根号）

答案解析收藏纠错 + 选题
16. (2023八下·普陀期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 相交于点O， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折后，点B落在点E处，联结 $\text{[math]}$ 、 $\text{[math]}$ ，那么四边形 $\text{[math]}$ 的周长 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

17. (2023八下·志丹期末) 如图，矩形纸片 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
18. (2023九上·太原月考) 如图，将矩形ABCD沿对角线AC折叠，点B的对应点为点E ， AE与CD交于点F ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
19. (2023·大安模拟) 某数学活动小组在学完特殊的平行四边形之后，针对矩形中的折叠问题进行了研究．
如图 $\text{[math]}$ ，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点，将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 为点 $\text{[math]}$ 折叠后的对应点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交折痕 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）猜想四边形 $\text{[math]}$ 的形状，并证明你的结论；
2. （2）如图 $\text{[math]}$ ，连接 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 上时， $\text{[math]}$ 的长为 $\text{[math]}$ 用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ；
3. （3）如图 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 上时，若 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2023八上·绍兴期中) 如图1，四边形ABCD是正方形，E，F分别在边BC和CD上，且∠EAF＝45°，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法。小明为了解决线段EF，BE，DF之间的关系，将△ADF绕点A顺时针旋转90°后解决了这个问题。
1. （1）请直接写出线段EF，BE，DF之间的关系.
2. （2）如图3，等腰直角三角形ABD，∠BAD=90°，AB=AD，点E，F在边BD上，且∠EAF=45°，请写出EF，BE，DF之间的关系，并说明理由.
答案解析收藏纠错 + 选题

四、实践探究题

21. (2023九上·丰满期中)
1. （1）【模型感知】如图①，在正方形ABCD中，点E是对角线AC上一点（不与点A、C重合），连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE^' ，求证：AE'＝CE；
2. （2）【模型发展】如图②，在正方形ABCD中，点E是对角线CA的延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE'，线段AE^'与CE的数量关系为，AE'与CE所在直线的位置关系为（不需证明）；
3. （3）【解决问题】如图③，在正方形ABCD中，点E是对角线AC延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°，得到线段BE'，连接AE'，EE'，若AC＝3CE ，则 $\text{[math]}$ ＝．
答案解析收藏纠错 + 选题
22. (2023九上·江源月考) 如图①．四边形ABCD与四边形AEFG是共一个顶点的两个大小不同的正方形．
1. （1）操作发现：如图②．正方形AEFG绕顶点A逆时针旋转，使点E落在边AD上时．填空：
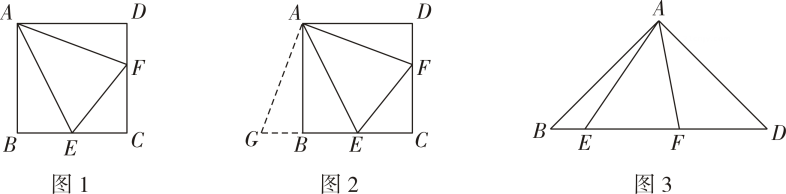
  ①线段BE与IG的数量关系是
  ②∠ABE与∠ADG的关系是
2. （2）猜想与证明：如图③，正方形AEFG绕顶点A逆时针旋转某一角度α（0<α< 90°）时．猜想（1）中的结论是否成立？并证明你的结论：
3. （3）拓展应用：如图④．正方形AEFG绕顶点A逆时针旋转，使点F落在边AD上时，若AB= $\text{[math]}$ ． AF=1，则BE=
答案解析收藏纠错 + 选题
23. (2024九上·宁江期末)
1. （1）【性质探究】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， AB＝AC ，点D在斜边BC上，将△ABD绕点A逆时针旋转90°得到△ACE．
  ①直线BD与CE的位置关系为；
  ②若点F为BE的中点，连接AF ，请探究线段AF与CD的数量关系，并给予证明．
2. （2）【拓展应用】
  如图2，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG ，连接BG，点H为BG的中点，连接AH ．若AB＝4，BE＝3，求AH的长．
答案解析收藏纠错 + 选题
24. (2023七下·巩义期末) 综合与实践
问题背景：
数学课上，同学们以“长方形纸带的折叠”为主题开展数学活动，已知长方形纸带的边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为线段AD上一动点 $\text{[math]}$ ，将纸片折叠，使点B和点 $\text{[math]}$ 重合，产生折痕EF，点E是折痕与边AD的交点，点F是折痕与边BC的交点．

动手操作：
1. （1）如图1，若点E与点A重合时，则 $\text{[math]}$ 的度数为．
  实践探究：
2. （2）如图2，移动点 $\text{[math]}$ ，其余条件不变．
  ①小静发现图中无论点 $\text{[math]}$ 如何移动， $\text{[math]}$ 始终成立，请说明理由；
  ②小东发现折叠后所形成的角，只要知道其中一个角的度数，就能求出其它任意一角的度数，若 $\text{[math]}$ ，求 $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题

五、综合题

25. (2023八下·尤溪月考) 如图，在平面直角坐标系中，A（－2，0），B（3，－1），C（2，2），网格中每一格的边长均为一个单位长度，请解答以下问题.
1. （1）请在图中作出△ABC.
2. （2）将△ABC平移，使得平移后点C的对应点为原点，点A、B的对应点分别为 $\text{[math]}$ ， $\text{[math]}$ ，请作出平移后的 $\text{[math]}$ ，并直接写出△ABC在CO方向上平移的距离.
3. （3）将△ABC绕点A逆时针旋转90°，得到 $\text{[math]}$ ，点B、C的对应点分别为 $\text{[math]}$ 、 $\text{[math]}$ ，请作出 $\text{[math]}$ ，并直接写出点 $\text{[math]}$ ， $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
26. (2023八下·龙江期中) 在 $\text{[math]}$ 中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC．
1. （1）如图1，若∠ADC=90°，G是EF的中点，连接AG、CG.
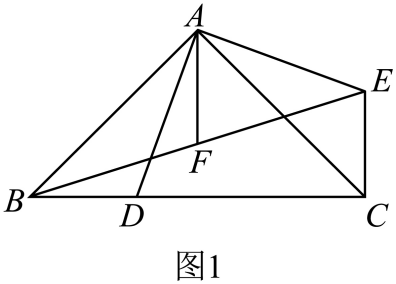
  ①求证：BE=BF；
  ②请判断△AGC的形状，并说明理由.
2. （2）如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG，判断△AGC的形状.（直接写出结论不必证明）
答案解析收藏纠错 + 选题
27. (2023八上·鄞州期末) 如图，在△ABC中，E是AB中点，F是AC上一动点，连结EF，将△AEF沿直线EF折叠得△DEF．
1. （1）如图①，若∠B=45°，且点D恰好落在线段BC上，求证：点F为线段AC的中点；
2. （2）如图②，若△ABC为等边三角形，且边长为4，当点D落在线段CE上时，求AF的长度；
3. （3）如图③，若△ABC为直角三角形，∠BAC=90°，AC=8．连结AD、BD、CD，若△ACD与△BDC面积相等，且CD=4，求△ABC的面积．
答案解析收藏纠错 + 选题
28. (2023七下·镇海期中) 如图，有一长方形纸带，E、F分别是边AD、BC上一点， $\text{[math]}$ 且 $\text{[math]}$ ，将纸带ABCD沿EF折叠成图1，再沿GF折叠成图2.
1. （1）当οα=25时，则∠FGD'=，∠GFC'=；
2. （2）两次折叠后，求∠NFE的大小（用含α的代数式表示）；
3. （3）当∠NFE和∠DEF的度数之和为100°时，求α的值.
答案解析收藏纠错 + 选题