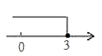
 B .
B .  C .
C . 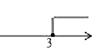 D .
D . 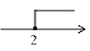

![]()
-4,-|-|,0,
, 2 013,-(+5),+1.88,0.010 010 001…(相邻两个1之间0的个数逐次加1),-2.33,….
整数集合{ };
非负数集合{ };
分数集合{ };
无理数集合{ }.

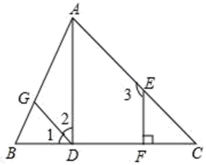
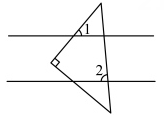
解:∵∠1=∠C,(已知)
∴GD∥ ▲ . ( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC=∠ ▲ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
大家知道是无理数,而无理数是无限不循环小数,因此
的小数部分我们不可能全部写出来,于是小明用
来表示
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:因为 , 即
, 所以
的整数部分为2,小数部分为
.
请解答下列问题: