备考2024年中考数学时事热点抢分练9 传染病及其防控

更新时间：2024-06-02 浏览次数：36 类型：三轮冲刺

一、选择题

1. (2020七上·舒城月考) 新型冠状病毒肺炎是一种新型的呼吸道传染病，美国因政府防控措施不力导致新型冠状病毒肺炎在其国内长时间传播，现在距约翰斯霍普金斯大学统计，美国已感染新型冠状病毒肺炎人数达到920万人之多，而且还在趁较快传染速度传播，已有超过22万人死亡．请用科学记数法将920万用科学记数法表示（）

A . 9.2× $\text{[math]}$ B . 9.2× $\text{[math]}$ C . 9.2× $\text{[math]}$ D . 0.92× $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·禹城月考) 有一人患了传染病，经过两轮传染后共有81人患病，则每轮传染中平均一个人传染的人数为（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
3. (2022七下·重庆市期中) 为预防传染病，某校定期对教室进行“药熏消毒”测出药物燃烧阶段室内每立方米空气中的含药量y（mg）和燃烧时间x（min）的数据如表：
燃烧时间x（min）
2.5
5
7.5
10
含药量y（mg）
2
4
6
8
则下列叙述错误的是（）

A . 燃烧时间为14min时，室内每立方米空气中的含药量为10mg B . 在一定范围内，燃烧时间越长，室内每立方米空气中的含药量越大 C . 室内每立方米空气中的含药量是因变量 D . 燃烧时间每增加2.5min，室内每立方米空气中的含药量增加2mg

答案解析收藏纠错 + 选题
4. (2021九上·龙江期末) 2019年12月以来，湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病．感染者的临床表现为：以发热、乏力、干咳为主要表现．在“新冠”初期，有1人感染了“新冠”，经过两轮传染后共有144人感染了“新冠”（这两轮感染因为人们不了解病毒而均未被发现未被隔离），则每轮传染中平均一个人传染了（）

A . 10人 B . 11人 C . 12人 D . 13人

答案解析收藏纠错 + 选题
5. (2020·福田模拟) 某市疾控中心在对10名传染病确诊病人的流行病史的调查中发现，这10人的潜伏期分别为：5，5，5，7，7，8，8，9，11，14（单位：天），则下列关于这组潜伏期数据的说法中，不正确的是（））

A . 众数是5天 B . 中位数是7.5天 C . 平均数是7.9天 D . 标准差是2.5天

答案解析收藏纠错 + 选题
6. (2021·福田模拟) 有一个模拟传染病传播的电子游戏模型：在一个方框中，先放入足够多的白球（模拟健康人），然后在框中同时放入若干个红球（模拟最初感染源）；程序设定，每经过一分钟，每个红球均恰好能使方框中R₀个白球同时变成红球（R₀为程序设定的常数）．若最初放入的白球数为400个，红球数为4个，从放入红球开始，经过2分钟后，红球总数变为了64个．则R₀应满足的方程是（　　）

A . 4（1+R₀）＝64 B . 4（1+R₀）＝400 C . 4（1+R₀）²＝64 D . 4（1+R₀）²＝400

答案解析收藏纠错 + 选题
7. 春季是传染病多发的季节，积极预防传染病是学校高度重视的一项工作，为此，某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中，先经过 $\text{[math]}$ 的集中药物喷洒，再封闭宿舍 $\text{[math]}$ ，然后打开门窗进行通风，室内每立方米空气中含药量 $\text{[math]}$ 与药物在空气中的持续时间 $\text{[math]}$ 之间的函数关系，在打开门窗通风前分别满足两个一次函数，在通风后又成反比例，如图所示.下面四个选项中错误的是（）

A . 经过集中喷洒药物，室内空气中的含药量最高达到 B . 室内空气中的含药量不低于的持续时间达到了 C . 当室内空气中的含药量不低于且持续时间不低于35分钟，才能有效杀灭某种传染病毒.此次消毒完全有效 D . 当室内空气中的含药量低于时，对人体才是安全的，所以从室内空气中的含药量达到开始，需经过后，学生才能进入室内

答案解析收藏纠错 + 选题

二、填空题

8. (2023九上·宣化期中) 某种传染病，若有一人感染，经过两轮传染后将共有49人感染.设这种传染病每轮传染中平均一个人传染了x个人，列出方程为.

答案解析收藏纠错 + 选题
9. (2023·鹿城模拟) 为预防传染病，某校定期对教室进行“药熏消毒”.如图所示，药物燃烧阶段，教室内每立方米空气中的含药量 $\text{[math]}$ 与燃烧时间x（分）成正比例；燃烧后，y与x成反比例.若 $\text{[math]}$ ，则x的取值范围是.

答案解析收藏纠错 + 选题
10. (2021七下·青岛期末) $\text{[math]}$ 型口罩可以帮助人们预防传染病．“ $\text{[math]}$ ”表示此类型的口罩能过滤空气中 $\text{[math]}$ 的粒径约为 $\text{[math]}$ 的非油性颗粒，其中，0.00000034用科学记数法表示为．

答案解析收藏纠错 + 选题
11. (2020八下·哈尔滨月考) 鸡瘟是一种传播速度很快的传染病，一轮传染为一天时间，红光养鸡场于某日发现一例，两天后发现共有169只鸡患有这种病，若每例病鸡传染健康鸡的只数均相同，则每只病鸡传染健康鸡只．

答案解析收藏纠错 + 选题
12. (2022·房山模拟) 为确定传染病的感染者，医学上可采用“二分检测方案”．假设待检测的总人数是 $\text{[math]}$ （ $\text{[math]}$ 为正整数）．将这 $\text{[math]}$ 个人的样本混合在一起做第1轮检测（检测1次），如果检测结果是阴性，可确定这些人都未感染；如果检测结果是阳性，可确实其中感染者，则将这些人平均分成两组，每组 $\text{[math]}$ 个人的样本混合在一起做第2轮检测，每组检测1次．依此类推：每轮检测后，排除结果为阴性的组，而将每个结果为阳性的组再平均分成两组，做下轮检测，直至确定所有的感染者．
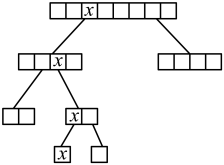
例如，当待检测的总人数为8，且标记为“ $\text{[math]}$ ”的人是唯一感染者时，“二分检测方案”可用如图所示．从图中可以看出，需要经过4轮共 $\text{[math]}$ 次检测后，才能确定标记为“ $\text{[math]}$ ”的人是唯一感染者．
1. （1） n的值为；
2. （2）若待检测的总人数为8，采用“二分检测方案”，经过4轮共9次检测后确定了所有的感染者，写出感染者人数的所有可能值；
答案解析收藏纠错 + 选题

三、综合题

13. (2023九上·长顺期末) 高致病性禽流感是一种传染性极强的传染病．
1. （1）养殖场有4万只鸡 $\text{[math]}$ 假设有一只鸡得了禽流感，如果不采取任何措施，那么第二天将新增病鸡10只，到第三天又将新增病鸡100只，以后每天新增病鸡数依此类推，请问到第四天，共有多少只鸡得了禽流感？到第几天，所有的鸡都会感染禽流感？
2. （2）为防止禽流感蔓延，防疫部门规定，离疫点3千米范围内为捕杀区 $\text{[math]}$ 所有的禽类全部捕杀 $\text{[math]}$ 离疫点 $\text{[math]}$ 千米范围内为免疫区，所有的禽类强制免疫；同时对捕杀区和免疫区的村庄，道路实行全封闭管理 $\text{[math]}$ 现有一条笔直的公路 $\text{[math]}$ 通过禽流感病区 $\text{[math]}$ 如图所示， $\text{[math]}$ 为疫点，到公路 $\text{[math]}$ 的最短距离为1千米，问这条公路在该免疫区内有多少千米？ $\text{[math]}$ 结果保留根号 $\text{[math]}$
答案解析收藏纠错 + 选题
14. (2023七下·志丹月考) 甲流指甲型流感，是由甲型流感病毒引起的急性呼吸道传染病．为了预防甲型流感病毒的扩散，学校准备购买一批医用口罩和洗手液用于日常防护，若买510个医用口罩比买16瓶洗手液贵8元；若买700个医用口罩比买24瓶洗手液便宜40元．
1. （1）求医用口罩和洗手液的单价；
2. （2）学校本次采购准备了800元，除购买医用口罩和洗手液外，还需再购买单价为3.8元/个的N95口罩a个，医用口罩和N95口罩共600个，购买洗手液b瓶，钱恰好全部用完，学校一共有几种购买方案？写出所有购买方案．
答案解析收藏纠错 + 选题
15. (2023八下·滨江期末) 为预防传染病，某校定期对教室进行“药熏消毒”．已知某种药物在燃烧阶段，室内每立方米空气中的含药量 $\text{[math]}$ 与燃烧时间 $\text{[math]}$ 成正比例；一次性燃烧完以后，y与x成反比例（如图所示）．在药物燃烧阶段，实验测得在燃烧5分钟后，此时教室内每立方米空气含药量为 $\text{[math]}$ ．
1. （1）若一次性燃烧完药物需10分钟．
  ①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式．
  ②当每立方米空气中的含药量低于 $\text{[math]}$ 时，对人体方能无毒害作用，那么从消毒开始，在哪个时间段学生不能停留在教室里？
2. （2）已知室内每立方米空气中的含药量不低于 $\text{[math]}$ 时，才能有效消毒，如果有效消毒时间要持续120分钟，问要一次性燃烧完这种药物需多长时间？
答案解析收藏纠错 + 选题
16. (2022八下·定远期末) 春季是传染病的高发期，某校为了调查学生对传染病预防知识的了解情况，从全校学生中随机抽取了部分学生进行相关知识的测试，并将测试成绩（x）分为五个等级：A（ $\text{[math]}$ ），B（ $\text{[math]}$ ），C（ $\text{[math]}$ ），D（ $\text{[math]}$ ），E（ $\text{[math]}$ ），整理后分别绘制成如图所示的频数直方图和扇形统计图（部分信息不完整）
1. （1）求测试等级为C的学生人数，井补全频数直方图
2. （2）求扇形统计图中等级为B所对应的扇形圆心角的度数：
3. （3）若全校1200名学生都参加测试，请根据抽样测试的结果，估计该校测试不低于80分的学生有多少人？
答案解析收藏纠错 + 选题
17. (2022八下·鄞州期末) 为预防传染病，某校定期对教室进行“药熏消毒”。如图，药物燃烧阶段，室内每立方米空气中的含药量y（毫克）与燃烧时间x（分）成正比例，10分钟时药物燃尽，此时教室内每立方米空气含药量为8毫克．燃尽后y与x成反比例．．
1. （1）求第5分钟时教室内每立方米空气中的含药量：
2. （2）画出药物燃尽后y关于x的反比例函数图象；
3. （3）当每立方米空气中含药量低于1.6毫克时，对人体方能无毒害作用，那么从消毒开始，在哪个时段学生不能停留在教室里？
答案解析收藏纠错 + 选题
18. (2021八上·徐汇期末) 接种疫苗是预防控制传染病最有效的手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a天接种后，由于情况变化，接种速度放缓．图中的折线BCD和线段OA分别反映了甲、乙两地的接种人数y（万人）与接种时间x（天）之间的函数关系．根据图像所提供的信息回答下列问题
1. （1）乙地比甲地提前了天完成疫苗接种工作．
2. （2）试写出乙地接种人数 $\text{[math]}$ （万人）与接种时间x（天）之间的函数解析式．
3. （3）当甲地放缓接种速度后，每天可接种万人．
答案解析收藏纠错 + 选题
19. (2022·上思模拟) R0，也叫基本传染数，或者基本再生数，英文为Basic reproduction number.更确切的定义是：在没有外力介入，所有人都没有免疫力的情况下，一个感染某种传染病的人，总共会传染给其他多少个人的平均数.最近，新型冠状病毒变异出德尔塔＋毒株，德尔塔＋变异病毒的R0值极高.若1人患病，在无任何外力影响下经历两轮传染后共有73人感染.
1. （1）求德尔塔＋变异病毒的R0值；
2. （2）国家研制出新冠疫苗后发现，通过接种疫苗可以使得R0值随接种人数比例的增高同步降低.例如，当疫苗全民接种率达到40%时，此时的R0值也下降40%.若有1人感染德尔塔＋变异病毒，要在两轮内将总感染人数控制在7人以内，再加以隔离等措施的干涉，就可控制住疫情，则全民接种率至少应该达到多少？
答案解析收藏纠错 + 选题
20. (2019九上·天台月考) 某学校在校师生及工作人员共600人，其中一个学生患了某种传染病，经过两轮传染后共有64人患了该病。
1. （1）求每轮传染中平均一个人传染了几个人？
2. （2）如果不及时控制，第三轮传染后学校还有多少人未被传染？
答案解析收藏纠错 + 选题
21. (2020八下·瑞安期中) 2019年12月以来，湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病.感染者的临床表现为：以发热、乏力、干咳为主要表现.约半数患者多在一周后出现呼吸困难，严重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍.
1. （1）在“新冠”初期，有1人感染了“新冠”，经过两轮传染后共有144人感染了“新冠”（这两轮感染因为人们不了解病毒而均未被发现未被隔离），则每轮传染中平均一个人传染了几个人？
2. （2）后来举国上下众志成城，全都隔离在家.小玲的爷爷因为种的水果香梨遇到销滞难题而发愁，于是小玲想到了在微信朋友圈里帮爷爷销售香梨.香梨每斤成本为4元/斤，她发现当售价为6元/斤时，每天可以卖80斤.在销售过程中，她还发现一斤香梨每降价0.5元时，则每天可以多卖出10斤.为了最大幅度地增加销售量，而且每天要达到100元的利润，问小玲应该将售价定为多少元？
答案解析收藏纠错 + 选题
22. (2021九上·成都月考) R₀ ，也叫基本传染数，或者基本再生数，英文为Basicreproductionnumber.更确切的定义是：在没有外力介入，所有人都没有免疫力的情况下，一个感染某种传染病的人，总共会传染给其他多少个人的平均数.例如：有1人感染新型冠状病毒，若R₀＝3.50，则经两轮传染后感染新型冠状病毒的人数为：1+1×3.50+1×3.50×3.50≈17（人）.时下人心惶惶的新型冠状病毒的基本传染数据估计为3.30到5.40之间.请解答下列问题：
1. （1）若现有10人感染新型冠状病毒，则经历两轮传染后，感染新型冠状病毒的人数大约在什么范围内（直接写出结果，结果保留整数）？
2. （2）最近，新型冠状病毒变异出德尔塔毒株，德尔塔变异病毒的R₀值极高.若1人患病，在无任何外力影响下经历两轮传染后共有73人感染.
  ①求德尔塔变异病毒的R₀值；
  
  ②国家研制出新冠疫苗后发现，通过接种疫苗可以使得R₀值随接种人数比例的增高同步降低.例如，当疫苗全民接种率达到40%时，此时的R₀值为：R₀（1﹣40%）＝0.6R₀.若有1人感染德尔塔变异病毒，要在两轮内将总感染人数控制在7人以内，再加以隔离等措施的干涉，就可控制住疫情，则全民接种率至少应该达到多少？
答案解析收藏纠错 + 选题
23. (2022八下·仓山期末) 为认真做好新冠疫情防控，增强学生新冠疫情防控与传染病预防意识，培养学生的健康意识与公共卫生意识，某校数学兴趣小组的同学设计了“新冠疫情防控知识”问卷，并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况，他们将全部测试成绩分成A，B，C，D四组，绘制了如下统计图表：
“新冠疫情防控知识”问卷测试成绩统计表

组别

分数/分

频数

A

$\text{[math]}$

36

B

$\text{[math]}$

74

C

$\text{[math]}$

60

D

$\text{[math]}$

30

其中被抽取的学生的问卷测试成绩中，将B组分数按小到大整理后，B组后15个分数为：75，76，76，76，76，78，78，78，78，78，79，79，79，80，80.

依据以上统计信息解答下列问题：
1. （1）被抽取学生的问卷测验成绩的中位数是：.
2. （2）为了增强大家对新冠疫情防控知识的了解，学校组织每个班级学习相关知识，经过一段时间的学习后，再次对原来抽取的这些同学进行问卷测试，发现A组的同学平均成绩提高15分，B组的同学平均成绩提高10分，C组的同学平均成绩提高5分，D组的同学平均成绩没有变化，请估计学习后这些同学的平均成绩提高多少分？若把测试成绩超过85分定为优秀，这些同学再次测试的平均成绩是否达到优秀，为什么？
答案解析收藏纠错 + 选题
24. (2023·佳木斯模拟) 为有效预防传染病的传播，学校需购买甲、乙两种消毒液每天对班级进行消杀工作，经了解，每桶甲种消毒液的售价比乙种消毒液的售价多10元，学校用600元和400元采购了相同桶数的甲、乙两种消毒液．
1. （1）求甲、乙两种消毒液的售价分别是每桶多少元；
2. （2）由于消杀工作的需要，学校需再次购买两种消毒液共500桶，且甲种消毒液的桶数不少于乙种消毒液的桶数，求甲种消毒液购买多少桶时，所需资金总额最少，最少总金额是多少元？
3. （3）商家决定对甲、乙两种消毒液打九折销售，在（2）中所需资金总额最少的条件下，学校用节省下来的钱全部购进A，B两种高压喷壶．已知A种高压喷壶50元/个，B种高压喷壶80元/个，请直接写出购进方案．
答案解析收藏纠错 + 选题

四、实践探究题

25. (2023九上·瑞安开学考) 确定有效消毒的时间段
背景素材
预防传染病，某校定期对教室进行“药熏消毒”．已知药物释放阶段，室内每立方米空气中的含药量y（mg）与释放时间x（min）成一次函数；释放后，y与x成反比例如图1所示，且2min时，室内每立方米空气中的含药量y（mg）达到最大值．某兴趣小组记录部分y（mg）与x（min）的测量数据如表1．满足 $\text{[math]}$ 的自变量x（min）的取值范围为有效消毒时间段．
x
…
0.5
1
1.5
2
2.5
3
…
y
…
2.5
3
3.5
4
3.2
2.67
…
问题解决
1. （1）任务1
  确定y关于x的一次函数及反比例函数的表达式．
2. （2）任务2
  初步确定有效消毒时间段即自变量x的取值范围．
3. （3）任务3
  若实际生活中有效消毒时间段要求满足a≤x≤3a ，其中a为常数，请确定实际生活中有效消毒的时间段．
答案解析收藏纠错 + 选题