①;②
;③DE垂直平分AB;④
, 其中正确是( )






①求证:四边形是平行四边形;
②连接交
于点
, 求
的面积;
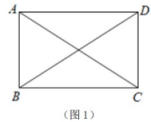
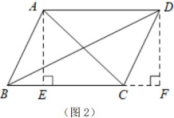
在探究平行四边形的性质时,学习小组利用这种思想方法,发现并证明了如下有趣结论,平行四边形两条对角线的平方和等于四边的平方和.请你根据学习小组的思路,完成下列问题:
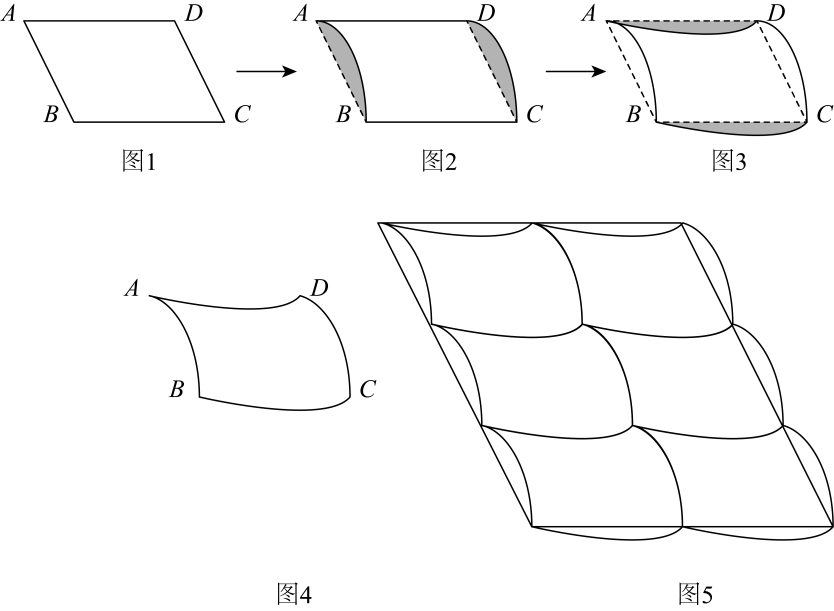
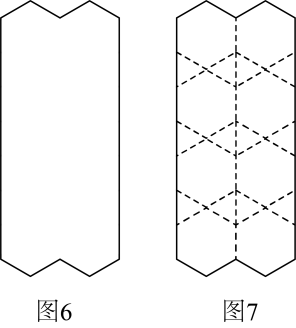
①请问两种瓷砖每块各多少元?
②小明对比两种瓷砖的价格后发现:用若干块边长为1的正三角形瓷砖和边长为1的正六边形瓷砖一起镶嵌总费用会更少.按小明的想法,将空白处全部镶嵌完,购买瓷砖最少需要 ▲ 元.

如图1,在中,
.
, 垂足为
, 点
在
上,连接
,
. 则有下列命题:①
;②
, 请你从中选择一个命题证明其真假,并写出证明过程.
如图2,在中,
,
, 点
在三角形的内部,过点
作
, 且
, 连接
. 求证:
.
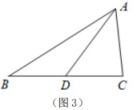
如图3.在中,
,
, 把线段
绕点
顺时针方向旋转
到
, 把线段
绕点
逆时针旋转
到
, 分别连接
,
,
, 请直接写出
面积的最大值.
例:已知 ,
, 其中
, 求证:
证明:
, 故

某游泳馆在暑假期间对学生优惠开放,有A,B两种方案可供选择,A方案:每次按原价打9折收费;B方案:前5次按照原价收费,从第6次起每次打8折.请问游泳的学生选择哪种方案更合算?
已知:如图1,D,E分别是等边的两边AB,AC上的点,且
CE.若BE,CD交于点
, 则
°;

如图2,已知点是等边
的AB边上一点,点
是AC延长线上一点,若
, 连接ED,EB.求证:
;

【拓展延伸】如图3,若点D,E分别是BA,AC延长线上一点,且.连接DE,以DE为边向右侧作等边
, 连接AF,求
的面积.

试猜想BD与CE的数量关系,并加以证明;
如图2,点D为等边内一点,将线段AD绕点A逆时针旋转60°得到线段AE,连接CE,若B、D、E三点共线,求证:EB平分
;
如图3,若是边长为2的等边三角形,点D是线段BC上的动点,将线段AD绕点D顺时针旋转60°得到线段DE,连接CE.点D在运动过程中,
的周长最小值=(直接写答案)

【特例分析】如图2,当恰好过点
, 且点
,
,
在同一条直线上时.


【理解】如图1,在平面直角坐标系中,的对角线
,
相交于点
, 若点
,
的坐标分别为
,
, 点
是
边上任意一点.
①(1)中的结论是否依然成立?请说明理由;
②若 ,
,连接
,当
时,求
的长.
