 B .
B . 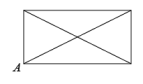 C .
C . 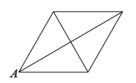 D .
D . 


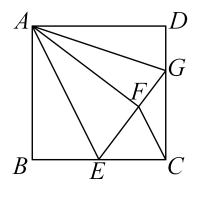

①;②
;③
;④
.
其中正确的结论是.(填写所有正确结论的序号)


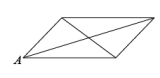
①猜想线段与
之间有怎样的数量和位置关系?请直接写出你的猜想,不需证明;
②下列结论:甲同学认为的值不变;乙同学认为:
的值不变,其中只有一个结论正确,请选择正确的结论并求其值;


①求证:;
②当的周长取最小值为
时,求
的周长;
勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.如图.

把两个全等的直角三角形如图1放置,其三边长分别为 ,
,
. 显然,
,
. 请用
,
,
分别表示出梯形
, 四边形
,
的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
,
,
,则它们满足的关系式为,经化简,可得到勾股定理.
借助上面的思考过程,画图说明并求代数式的最小值
.

①当CD=6.CE=4时,求BE的长;
②求证:CD=CH .