【提升版】北师大版数学九上第一章特殊的平行四边形单元...

更新时间：2024-07-09 浏览次数：37 类型：单元试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. (2024八下·寻甸期中) 如图，在菱形ABCD中，AC＝6cm，BD＝8cm，则菱形AB边上的高CE的长是（）

A . 4.8cm B . 9.6cm C . 5cm D . 10cm

答案解析收藏纠错 + 选题
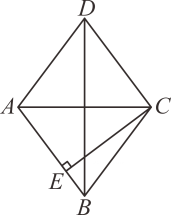
2. (2024八下·会昌期中) 如图，菱形OABC在平面直角坐标系中的位置如图所示，∠AOC＝45°，OA＝ $\text{[math]}$ ，则点C的坐标为（　　）

A . （ $\text{[math]}$ ， 1） B . （1，1） C . （1， $\text{[math]}$ ） D . （ $\text{[math]}$ +1，1）

答案解析收藏纠错 + 选题
3. (2024九上·江津期末) 如图，正方形 $\text{[math]}$ 的边长为4， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转 $\text{[math]}$ 得到 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
4. (2023九上·小店期中) 如图，四边形ABCD是正方形，在正方形内部作等边三角形EDC ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
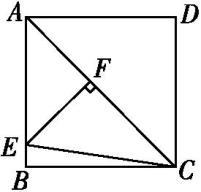
5. (2023九上·贵阳月考) 如图所示，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为（）

A . $\text{[math]}$ B . 3 $\text{[math]}$ C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
6. (2023九上·青白江期中) 如图，已知线段AB，按下列步骤作图：分别以A、B为圆心，大于 $\text{[math]}$ AB长为半径画弧，两弧相交于点M、N，作直线MN，交AB于点O，分别连接MA、MB、NA、NB，如果四边形MANB是正方形，需要添加的条件是（　　）

A . AO＝MO B . MA∥NB C . MA＝NB D . AB平分∠MAN

答案解析收藏纠错 + 选题
7. (2024九上·龙岗期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上一点，把 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，使点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·茂名期中) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一动点，过点 $\text{[math]}$ 分别作 $\text{[math]}$ 于点 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 2 B . 2.4 C . 2.5 D . 3

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·香洲期中)
如图，已知平行四边形ABCD中，AB=BC，BC=10，∠BCD=60°，两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动，连接OA，则OA的长的最小值是．

答案解析收藏纠错 + 选题
10. (2024八下·大祥期末) 如图，在正方形 $\text{[math]}$ 中，点F为 $\text{[math]}$ 上一点， $\text{[math]}$ 与 $\text{[math]}$ 交于点E．若 $\text{[math]}$ ，则 $\text{[math]}$ 等于度．

答案解析收藏纠错 + 选题
11. (2024八下·岳塘期中) 正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，那么 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
12. 如图，矩形ABCD的对角线AC、BD相交于点O，过点O作OE⊥BC，垂足为点E，过点A作AF⊥OB，垂足为点F，若BC＝2AF，OD＝6，则BE的长为．

答案解析收藏纠错 + 选题
13. (2023九上·达川月考) 如图，点G是正方 $\text{[math]}$ 边AB上一点，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点H ，当矩形 $\text{[math]}$ 与正方形 $\text{[math]}$ 面积相等时，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

14. (2023九上·都昌期中) 如图，在正方形ABCD中， $\text{[math]}$ ，请仅用无刻度的直尺画图（保留画图痕迹，不写画法）.
图① 图②
1. （1）在图①中，画出AD的中点M；
2. （2）在图②中，画出CD的中点N.
答案解析收藏纠错 + 选题
15. (2024九上·巴彦期末) 如图1，已知四边形 $\text{[math]}$ 是菱形，点E，F在对角线 $\text{[math]}$ 上， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，若 $\text{[math]}$ ，点E为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点O，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点G，在不添加任何辅助线情况下，请直接写出图2中等于线段 $\text{[math]}$ 的 $\text{[math]}$ 倍的四条线段．
答案解析收藏纠错 + 选题
16. (2024九上·哈尔滨期末) 在菱形 $\text{[math]}$ 中， $\text{[math]}$ 分别为 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，连接并延长 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）如图1，求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）如图2，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，请直接写出长为线段 $\text{[math]}$ 长2倍的线段．
答案解析收藏纠错 + 选题
17. (2023九上·都昌期中) 如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点.
1. （1）求证： $\text{[math]}$ .
2. （2）连接MQ、PN ，判断四边形MPNQ的形状，并说明理由.
3. （3）矩形ABCD的边AB与AD满足什么长度关系时，四边形MPNQ是正方形？请说明理由.
答案解析收藏纠错 + 选题
18. (2023九上·绥化期中) 如图，矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 的直线分别交 $\text{[math]}$ 、 $\text{[math]}$ 边于点 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
19. (2023九上·鄠邑期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 。
1. （1）求证： $\text{[math]}$ ；
2. （2）若正方形 $\text{[math]}$ 的边长是5， $\text{[math]}$ ，求 $\text{[math]}$ 的长。
答案解析收藏纠错 + 选题
20. (2024九上·涪城开学考) 如图，在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF=45° ，分别连接EF、BD ， BD与AF、AE分别相交于点M、N.
1. （1）求证：EF=BE+DF.为了证明“EF=BE+DF”，小明延长CB至点G ，使BG=DF ，连接AG ，请画出辅助线并按小明的思路写出证明过程.
2. （2）若正方形ABCD的边长为6，BE=2，求DF的长.
答案解析收藏纠错 + 选题