人教版八年级上学期数学第十一章质量检测（高阶）

更新时间：2024-08-09 浏览次数：87 类型：单元试卷

一、选择题

1. (2024八下·卫东期中) 多边形的每一个外角都是 $\text{[math]}$ ，则此多边形从一个顶点出发的对角线有（）条.

A . 7条 B . 8条 C . 9条 D . 10条

答案解析收藏纠错 + 选题
2. (2023八上·献县月考) 小明把一副直角三角尺按如图所示的方式摆放在一起，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八上·温岭竞赛) 五条长度均为整数厘米的线段：a₁ ， a₂ ， a₃ ， a₄ ， a₅ ，满足a₁＜a₂＜a₃＜a₄＜a₅ ，其中a₁＝1厘米，a₅＝9厘米，且这五条线段中的任意三条都不能构成三角形，则a₃＝（）

A . 3厘米 B . 4厘米 C . 3或4厘米 D . 不能确定

答案解析收藏纠错 + 选题
4. (2020八上·南宁月考) 如图，在△ABC中，BE平分∠ABC交AC于点E ， CD⊥AC交AB于点D ， ∠BCD=∠A ，则∠BEA的度数（）

A . 155° B . 135° C . 108° D . 100°

答案解析收藏纠错 + 选题
5. (2019八上·涧西月考) 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（）

A . 180° B . 360 C . 270° D . 540°

答案解析收藏纠错 + 选题
6. (2018八上·芜湖期末) 如图，A，B，C分别是线段A₁B，B₁C，C₁A的中点，若△ABC的面积是1，那么△A₁B_lC₁的面积是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
7. (2024八上·临江期末) 有一块直角三角尺DEF放置在△ABC上，三角尺DEF的两条直角边DE ， DF恰好分别经过点B ， C ．在△ABC中，若 $\text{[math]}$ ，则∠A的度数是（）

A . 40° B . 44° C . 45° D . 50°

答案解析收藏纠错 + 选题
8. 如图，∠ABC=∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF，以下结论：①AD∥BC，②∠ACB=∠ADB，③∠ADC+∠ABD = 90°， ④∠ADB= 45°-∠CDB，其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2021八上·迁安期中) 如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于EF两点，∠BAC∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI.下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2022八上·科尔沁期末) 如图，已知 $\text{[math]}$ 的内角 $\text{[math]}$ ，分别作内角 $\text{[math]}$ 与外角 $\text{[math]}$ 的平分线，两条平分线交于点 $\text{[math]}$ ，得 $\text{[math]}$ ； $\text{[math]}$ 和 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ，得 $\text{[math]}$ ；……以此类推得到 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2019八上·景县月考) 如图，小明从A点出发前进10m，向右转15°，再前进10 m，又向右转15°，…，这样一直走下去，他第一次[回到出发点A时，一共走了m。

答案解析收藏纠错 + 选题
12. (2020八上·中山期中) 如图，已知△ABC是等边三角形，点O是BC上任意一点，OE⊥AB，OF⊥AC，等边三角形的高为2，则OE+OF的值为.

答案解析收藏纠错 + 选题
13. (2019八上·长兴月考) 如图，△ABC的面积为18，BD=2DC，AE=2EC，那么阴影部分的面积是。

答案解析收藏纠错 + 选题
14. (2020八上·商城月考) 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t=，△APE的面积等于6．

答案解析收藏纠错 + 选题
15. 如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为．

答案解析收藏纠错 + 选题

三、解答题

16. (2023八上·凤凰月考) 小明在计算某个多边形的内角和时，由于粗心他漏掉一个内角，求得内角和 $\text{[math]}$ ，你能否求得他漏掉的内角度数和多边形内角和的正确结果吗？

答案解析收藏纠错 + 选题
17. (2023八上·龙马潭开学考) 如图，已知AD，AE分别是△ABC的高和中线，AB=3cm，AC=4cm，BC=5cm，∠CAB=90°，求：
1. （1） AD的长；
2. （2） △ACE和△ABE的周长的差．
答案解析收藏纠错 + 选题
18. (2023八上·诸暨月考) 如图1，已知∠MON=60° ， A、B两点同时从点O出发，点A沿射线ON运动，点B沿射线OM运动．，点C为△ABO三条内角平分线交点，连接BC、AC ．
1. （1）如图2，当∠OAB=70° ，求∠ACB的大小。
2. （2）在点A、B的运动过程中，∠ACB的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由：
3. （3）如图3，连接OC并延长，与∠ABM的角平分线交于点P ，与AB交于点Q ．在△BCP中，如果有一个角是另一个角的2倍，直接写出∠BAO的度数．
答案解析收藏纠错 + 选题
19. (2023八上·开州开学考) 阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”．例如：一个三角形三个内角的度数分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，这个三角形就是一个“梦想三角形”．反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍．
1. （1）如果一个“梦想三角形”有一个角为 $\text{[math]}$ ，那么这个“梦想三角形”的最小内角的度数为　　；
2. （2）如图1，已知 $\text{[math]}$ ，在射线 $\text{[math]}$ 上取一点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为端点作射线 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点 $\text{[math]}$ （点 $\text{[math]}$ 不与 $\text{[math]}$ 、 $\text{[math]}$ 重合），若 $\text{[math]}$ ．判定 $\text{[math]}$ 　　“梦想三角形”（填是或者不是）
3. （3）如图2，点 $\text{[math]}$ 在 $\text{[math]}$ 的边上，连接 $\text{[math]}$ ，作 $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点 $\text{[math]}$ ，在 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ 是“梦想三角形”，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题

四、实践探究题

20. (2023八上·南昌月考)
1. （1）【课本再现】如图1，在 $\text{[math]}$ 中，线 $\text{[math]}$ 经过点 $\text{[math]}$ 且 $\text{[math]}$ ．求证： $\text{[math]}$ ；
2. （2）【变式演练】如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
3. （3）【方法应用】如图3，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，夹角的锐角为 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上且在点 $\text{[math]}$ 右侧，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上且在直线 $\text{[math]}$ 上方，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上且在点 $\text{[math]}$ 左侧运动，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动（不与点 $\text{[math]}$ 重合）．当 $\text{[math]}$ 时， $\text{[math]}$ 平分 $\text{[math]}$ 平分 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
21. (2023八上·日照月考) 探究与发现：
1. （1）如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ．
  ①若 $\text{[math]}$ ，则 $\text{[math]}$ ；
  ②若 $\text{[math]}$ ，用含有 $\text{[math]}$ 的式子表示 $\text{[math]}$ 的度数为；
2. （2）如图2，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ，试探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；
3. （3）如图3，在六边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．
答案解析收藏纠错 + 选题
22. (2023八上·兴宁开学考)
1. （1）【问题背景】小强在学习完平行线一节后，想利用平行线的知识证明“三角形的内角和是180°”；．如图1，是小强为证明三角形内角和是180°所采取的构图方法：过△ABC的顶点A作EF∥BC ．
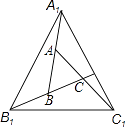
  请完成：利用小强的构图，说明∠BAC+∠B+∠C＝180°的理由；
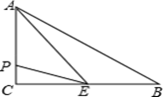
2. （2）【尝试应用】如图2，直线l₁与直线l₂相交于点O ，夹角为α，点B在点O右侧，点C在l₁上方，点A在O点左侧运动，点E在射线CO上运动（不与C ， O重合）；
  请完成：当α＝60°时，AG平分∠EAB ， EF平分∠AEC交直线AG于点G ，求∠AGE的度数；
3. （3）【拓展创新】如图3，点E在线段CO上运动（不与C ， O重合），∠AEF＝n∠AEC ， ∠EAG＝m∠EAB ， m+2n＝1，EF交AG于点G；
  请完成：当n为何值时，∠AGE不随∠EAB的变化而变化，并用含α的代数式表示∠AGE的度数（写出解答过程）．
答案解析收藏纠错 + 选题
23. (2024八上·南山期末) 【问题呈现】
如图①，已知线段 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ ，我们把形如这样的图形称为“ $\text{[math]}$ 字型”．
1. （1）证明： $\text{[math]}$ ．
2. （2）【问题探究】
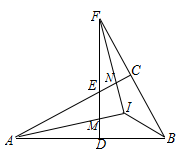
  继续探究，如图②， $\text{[math]}$ 、 $\text{[math]}$ 分别平分 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系．为了研究这一问题，尝试代入 $\text{[math]}$ 、 $\text{[math]}$ 的值求 $\text{[math]}$ 的值，得到下面几组对应值：
  表中 $\text{[math]}$ ，猜想得到 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 的数量关系为；
3. （3）证明（ $\text{[math]}$ ）中猜想得到的 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 的数量关系；
  $\text{[math]}$ （单位：度）
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$ （单位：度）
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$ （单位：度）
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

人教版八年级上学期数学第十一章质量检测（高阶）

副标题：

*注意事项：

人教版八年级上学期数学第十一章质量检测（高阶）

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$ （单位：度）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ （单位：度）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ （单位：度）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$