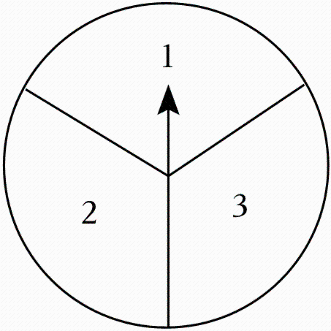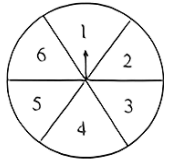

 B .
B . 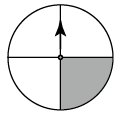 C .
C . 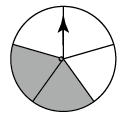 D .
D . 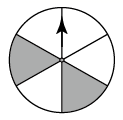



试验次数n | 20 | 40 | 60 | 80 | 100 | 1000 |
“指针落在灰色区域内”的次数m | 6 | 11 | 15 | 21 | 25 | 251 |
“指针落在灰色区域内”的频率 | 0.3 | 0.275 | 0.25 | 0.2625 | 0.25 | 0.251 |
根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率约是.(结果精确到0.01)

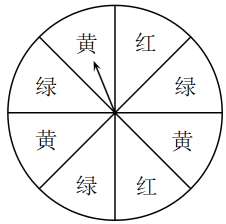
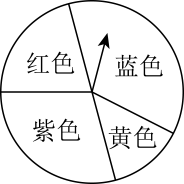

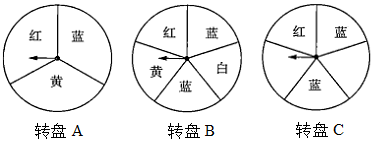


方案一:转动转盘一次,若指针指向数字1可领取一份奖品;
方案二:转动转盘两次,若两次指针指向的数字之和为奇数可领取一份奖品.(若指针指向分界线,则重转)