



①求证:;
②若 ,
,
, 求
与
的值.
如图(1),在四边形ABCD中,对角线AC⊥BD,垂足为点P.求证:S四边形ABCD= AC•BD;
证明:∵AC⊥BD,
∴
∴S四边形ABCD=S△ACD+S△ACB= AC•PD+
AC•BP
= AC(PD+PB)=
AC•BD
解答问题:

阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出的值.


图1 图2 图3

在绝妙四边形ABCD中,AC垂直平分BD , 若∠BAD=80°,则∠BCD=;
如图,在梯形ABCD中,AD∥BC , AB=AD=CD , ∠B=72°.
求证:梯形ABCD是绝妙四边形.
折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船等,折纸活动也伴随着我们初中数学的学习在折纸过程中,我们可以通过研究图形的性质和运动、确定图形位置等,进一步发展空间观念,在经历借助图形思考问题的过程中,我们会初步建立几何直观,折纸往往从矩形纸片开始,今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论.
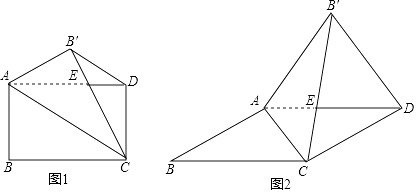
【实践操作】
如图1,将矩形纸片ABCD沿对角线AC翻折,使点B′落在矩形ABCD所在平面内,B'C和AD相交于点E,连接B′D.
①B′D和AC的位置关系为;
②将△AEC剪下后展开,得到的图形是;