 C .
C . ![]()
 B .
B .  C .
C .  D .
D . 

根据统计图提供的信息,下列推断合理的是( )
| 抛掷次数n | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| “正面向上”次数m | 22 | 52 | 71 | 95 | 116 | 138 | 160 | 187 | 214 | 238 |
| “正面向上”频率 | 0.44 | 0.52 | 0.47 | 0.48 | 0.46 | 0.46 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的概率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是( )


|
科目 |
思想品德 |
历史 |
地理 |
|
参考人数(人) |
19 |
13 |
18 |
其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有人;该班至少有学生人.

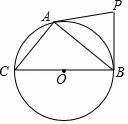
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ∥l.
作法:如图.
①在直线l上取两点A,B;
②以点P为圆心,AB为半径画弧,以点B为圆心,AP为半径画弧,两弧在直线l上方相交于点Q;
③作直线PQ.
根据小东设计的尺规作图过程
证明:PA=,AB=,
∴四边形PABQ是平行四边形
∴PQ∥l().(填写推理的依据)



小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
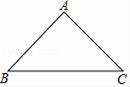
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点C向点B运动,点E以2cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为xcm,D,E两点间的距离为ycm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:

|
x/cm |
0 |
1 |
2 |
3 |
4 |
5 |
|
y/cm |
6.0 |
4.8 |
3.8 |
|
2.7 |
3.0 |
(说明:补全表格时相关数值保留一位小数)

a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
| 平均数 | 方差 | 中位数 | |
| 甲 | 79.6 | 36.84 | 78.5 |
| 乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
| 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
| 出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
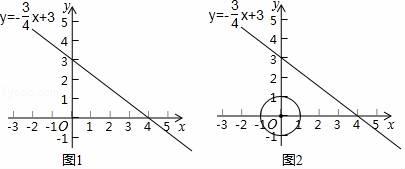
①如图1,求d(O,B)的最小值;
②如图2,C是以原点O为圆心,1为半径的圆上的一个动点,求d(B,C)的最小值.