

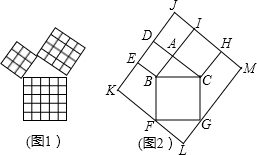
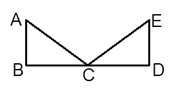

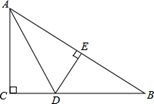
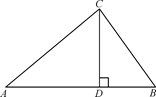
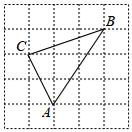
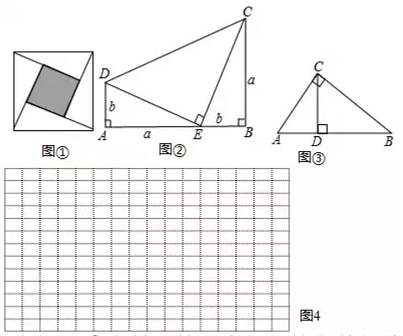
等腰直角三角形勾股高三角形(请填写“是”或者“不是”);

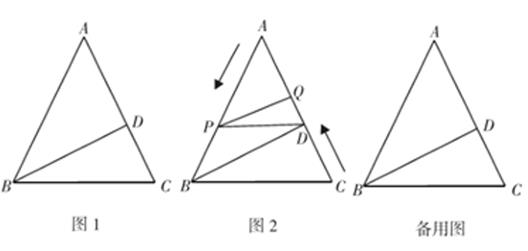
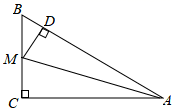
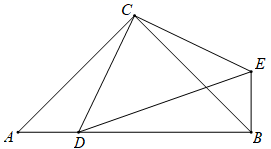
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB , CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;

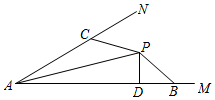
如图3,等腰△ABC为勾股高三角形,其中 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E . 若
,试求线段DE的长度.

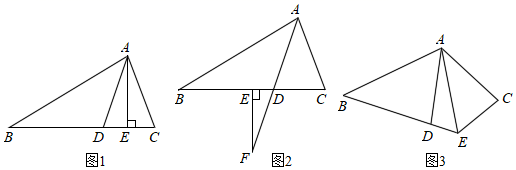
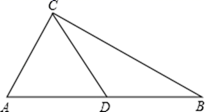
如图1, 中,
,
于点
,
且
;如图2,在图1的基础上,动点
从点
出发以每秒
的速度沿线段
向点
运动,同时动点
从点
出发以相同速度沿线段
向点
运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动的时间为
秒.