
 B .
B . 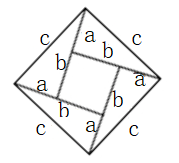 C .
C . 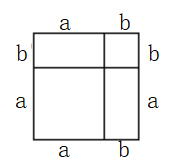 D .
D . 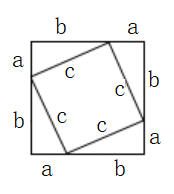
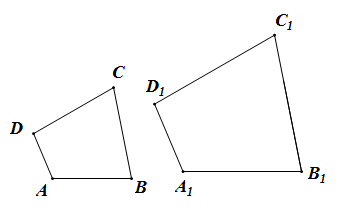
①四条边成比例的两个凸四边形相似;(命题)
②三个角分别相等的两个凸四边形相似;(命题)
③两个大小不同的正方形相似.(命题)
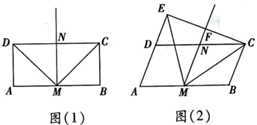
数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.
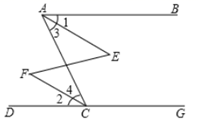
小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(小海的证法)证明:
是
的垂直平分线,
,(第一步)
,(第二步)
.(第三步)
四边形
是平行四边形.(第四步)
四边形
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)

求证:四边形ABCD是四边形.
在方框中填空,以补全已知和求证;
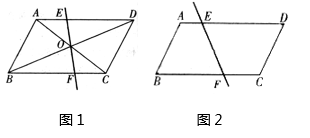
①求证:四边形ABFE与四边形CDEF的面积相等;
②经过以上证明,可以总结出平行四边形一个一般结论:过平行四边形对角线交点的任意一条直线,.
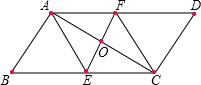
①如图2,已知点E ,F分别是平行四边形ABCD的边AD,BC上的两点,(点E ,F不与顶点重合),直线EF将平行四边形ABCD分成面积相等的两部分.
求证:直线EF经过平行四边形ABCD对角线的交点.
②直接回答:经过探究得知(1)②中的命题的逆命题是真命题还是假命题?
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1:
这个图形的面积可以表示成:
(a+b)2或a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
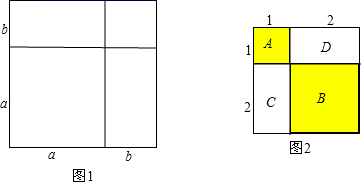
类比解决:
问题提出:如何利用图形几何意义的方法证明:13+23=32?
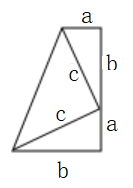
如图2,A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
请用上面的表示几何图形面积的方法探究:13+23+33+…+n3=.(直接写出结论即可,不必写出解题过程)
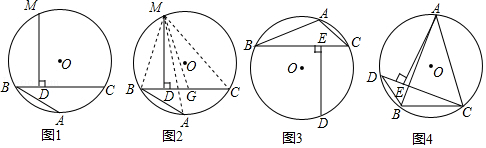
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG
∵M是 的中点,
∴MA=MC
……
①如图3,已知△ABC内接于⊙O,BC>AB>AC,D是 的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为;
②如图4,已知等腰△ABC内接于⊙O,AB=AC,D为 上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4
+2,BC=2,请求出AC的长.