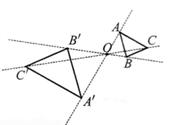









②以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在网格内画出△A2B2C2;
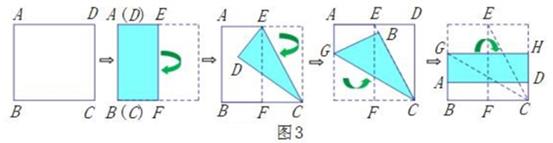
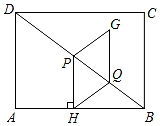
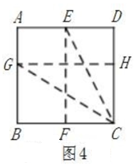
如图4所示,按上述方法折叠所得到的折痕GH是否为正方形ABCD的黄金线?请说明理由。
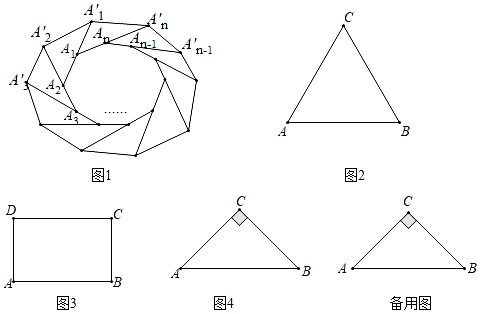
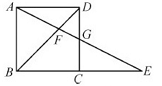
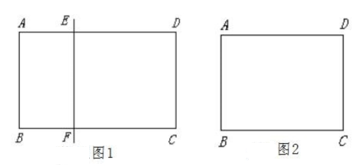
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
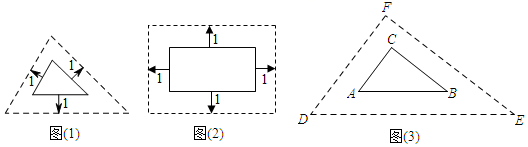
请回答下列问题:
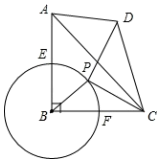
②连接DB,对角线DB交PQ于点O,若点O恰好为PQ的三等分点,请直接写出 的值.