2021-2022学年北师版数学八年级上册期末模拟试题一

更新时间：2021-12-04 浏览次数：164 类型：期末考试

一、单选题

1. (2021·毕节) 下列说法正确的是（）

A . 了解市民知晓“礼让行人”交通新规的情况，适合全面调查 B . 一组数据5，5，3，4，1的中位数是3 C . 甲、乙两人9次跳高成绩的方差分别为 $\text{[math]}$ _甲² $\text{[math]}$ ， $\text{[math]}$ _乙² $\text{[math]}$ ，说明乙的成绩比甲稳定 D . “经过有交通信号灯的路口，遇到红灯”是随机事件

答案解析收藏纠错 + 选题
2. (2021八上·临泉期末) 将一副三角板按如图所示的位置摆放在直尺上，则 $\text{[math]}$ 的度数为（）

A . 70° B . 75° C . 80° D . 85°

答案解析收藏纠错 + 选题
3. (2021·西藏) 如图，在Rt△ABC中，∠A＝30°，∠C＝90°，AB＝6，点P是线段AC上一动点，点M在线段AB上，当AM＝ $\text{[math]}$ AB时，PB＋PM的最小值为（）

A . 3 $\text{[math]}$ B . 2 $\text{[math]}$ C . 2 $\text{[math]}$ ＋2 D . 3 $\text{[math]}$ ＋3

答案解析收藏纠错 + 选题
4. (2023九下·遵义模拟) 下列无理数，与3最接近的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·新罗期中) 下列计算正确的是（）

A . $\text{[math]}$ 3 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . （ $\text{[math]}$ ）²＝2

答案解析收藏纠错 + 选题
6. (2023·南岗模拟) 一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返同，且往返速度的大小不变，两车离甲地的距离 $\text{[math]}$ （单位： $\text{[math]}$ ）与慢车行驶时间 $\text{[math]}$ （单位： $\text{[math]}$ ）的函数关系如图，则两车先后两次相遇的间隔时间是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·贵州) 已知直线 $\text{[math]}$ 与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴分别交于A、B两点，点P是第一象限内的点，若△PAB为等腰直角三角形，则点P的坐标为（）

A . （1，1） B . （1，1）或（1，2） C . （1，1）或（1，2）或（2，1） D . （0，0）或（1，1）或（1，2）或（2，1）

答案解析收藏纠错 + 选题
8. (2024七下·芙蓉期中) 九章算术中记载了一个问题，大意是：甲、乙两人各带了若干钱.若甲得到乙所有钱的一半，则甲共有钱50.若乙得到甲所有钱的 $\text{[math]}$ ，则乙也共有钱50.甲、乙两人各带了多少钱?设甲带了钱 $\text{[math]}$ ，乙带了钱 $\text{[math]}$ ，依题意，下面所列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九下·柳州期中) 关于x，y的方程组 $\text{[math]}$ 的解为 $\text{[math]}$ ，若点P（a，b）总在直线y＝x上方，那么k的取值范围是（）

A . k＞1 B . k＞﹣1 C . k＜1 D . k＜﹣1

答案解析收藏纠错 + 选题
10.
如图，一次函数y=k₁x+b₁的图象l₁与y=k₂x+b₂的图象l₂交于点A，则方程组 $\text{[math]}$ 的解是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2022·枣庄模拟) 一块含有45°的直角三角板和直尺如图放置，若∠1＝55°，则∠2的度数是（）

A . 30° B . 35° C . 40° D . 45°

答案解析收藏纠错 + 选题
12. (2021八下·栾城期末) 快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 $\text{[math]}$ 与它们的行驶时间 $\text{[math]}$ 之间的函数关系.小欣同学结合图像得出如下结论：
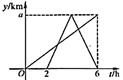
①快车途中停留了 $\text{[math]}$ ；②快车速度比慢车速度多 $\text{[math]}$ ；③图中 $\text{[math]}$ ；④快车先到达目的地.其中正确的是（）

A . ①③ B . ②③ C . ②④ D . ①④

答案解析收藏纠错 + 选题

二、填空题

13. (2024八下·赤坎期末) 在正比例函数 $\text{[math]}$ 中，y的值随着x值的增大而增大，则点 $\text{[math]}$ 在第象限.

答案解析收藏纠错 + 选题
14. (2021·阜新) 育红学校七年级学生步行到郊外旅行．七（1）班出发1h后，七（2）班才出发，同时七（2）班派一名联络员骑自行车在两班队伍之间进行联络，联络员和七（1）班的距离s（km）与七（2）班行进时间t（h）的函数关系图象如图所示．若已知联络员用了 $\text{[math]}$ 第一次返回到自己班级，则七（2）班需要 h才能追上七（1）班．

答案解析收藏纠错 + 选题
15. (2024九下·孝南模拟) 人们把 $\text{[math]}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的 $\text{[math]}$ 法就应用了黄金分割数.设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ，…， $\text{[math]}$ .则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2024七下·姜堰月考) 已知关于x，y的二元一次方程组 $\text{[math]}$ 满足 $\text{[math]}$ ，则a的取值范围是.

答案解析收藏纠错 + 选题
17. (2022·台儿庄模拟) 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

答案解析收藏纠错 + 选题
18. (2021·南京) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ .设 $\text{[math]}$ ，则 $\text{[math]}$ （用含 $\text{[math]}$ 的代数式表示）.

答案解析收藏纠错 + 选题

三、解答题

19. (2021八上·沈阳期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024八下·滨海月考) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2021七下·潼南期末) 解下列方程组：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题

22. (2022八下·枣阳期末) 为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛.为了解竞赛成绩，抽样调查了七，八年级部分学生的分数，过程如下：

（ 1 ）收集数据从该校七.八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（ 2 ）整理、描述数据按如下分段整理描述样本数据：

分数 $\text{[math]}$

人数

年级

$\text{[math]}$

七年级

八年级

$\text{[math]}$

（ 3 ）分析数据两组样本数据的平均数、中位数、众数、方差如下表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$\text{[math]}$	$\text{[math]}$	33.2

根据以上提供的信息，解答下列问题：

①填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙”）：

③从样本数据分析来看，分数较整齐的是年级（填“七”或“八”）；

④如果七年级共有400人参赛，则该年级约有人的分数不低于95分.

答案解析收藏纠错 + 选题

23. (2024七下·淮滨期末) 本地某快递公司规定：寄件不超过 $\text{[math]}$ 千克的部分按起步价计费；寄件超过 $\text{[math]}$ 千克的部分按千克计费.小丽分别寄快递到上海和北京，收费标准及实际收费如下表：
收费标准

目的地

起步价（元）

超过 $\text{[math]}$ 千克的部分

（元 $\text{[math]}$ 千克）

上海

$\text{[math]}$

$\text{[math]}$

北京

$\text{[math]}$

$\text{[math]}$

实际收费

目的地

质量

费用（元）

上海

2

9

北京

3

22

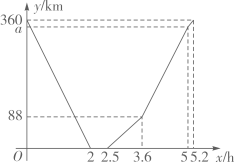
求 $\text{[math]}$ ， $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题
24. (2023八下·宜春期中) 小军到某景区游玩，他从景区入口处步行到达小憩屋，休息片刻后继续前行，此时观光车从景区入口处出发的沿相同路线先后到达观景点，如图， $\text{[math]}$ ， $\text{[math]}$ 分别表示小军与观光车所行的路程 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的关系.
根据图象解决下列问题：
1. （1）观光车出发分钟追上小军；
2. （2）求 $\text{[math]}$ 所在直线对应的函数表达式；
3. （3）观光车比小军早几分钟到达观景点？请说明理由.
答案解析收藏纠错 + 选题
25. (2017·达州)
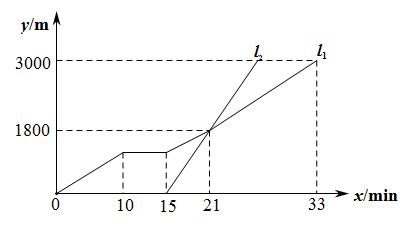
小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P₁（x₁ ， y₁），P₂（x₂ ， y₂），可通过构造直角三角形利用图1得到结论：P₁P₂= $\text{[math]}$ 他还利用图2证明了线段P₁P₂的中点P（x，y）P的坐标公式：x= $\text{[math]}$ ，y= $\text{[math]}$ ．
1. （1）请你帮小明写出中点坐标公式的证明过程；
2. （2） ①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；
  ②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：；
3. （3）
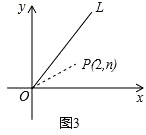
  如图3，点P（2，n）在函数y= $\text{[math]}$ x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．
答案解析收藏纠错 + 选题
26. (2020八上·太康期中) 如图，在等边三角形ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．
1. （1）（问题解决）
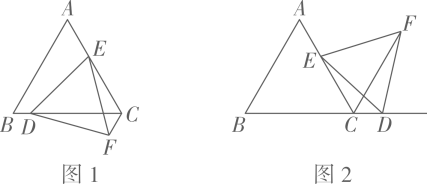
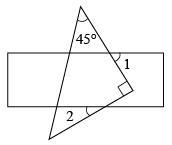
  如图1，若点D在边BC上，求证：CE+CF＝CD；
2. （2）（类比探究）
  如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
答案解析收藏纠错 + 选题