 B .
B .  C .
C .  D .
D . 
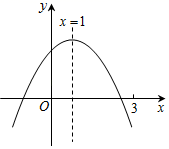
①函数 ,
在
上是“逼近函数”;②函数
,
在
上是“逼近函数”;③
是函数
,
的“逼近区间”;④
是函数
,
的“逼近区间”.其中,正确的有( )
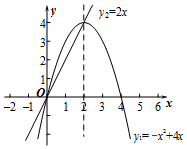
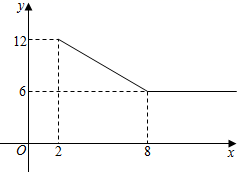
①当a=2时,求PB+PC的值;
②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.
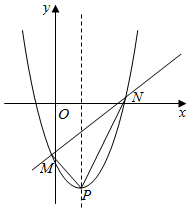
(Ⅰ)若二次函数的图象经过(3,﹣2),且对称轴为x=1,求二次函数的解析式;
(Ⅱ)如图,在(Ⅰ)的条件下,过定点的直线y=﹣kx+k﹣4(k≤0)与(1)中的抛物线交于点M,N,且抛物线的顶点为P,若△PMN的面积等于3,求k的值;
(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
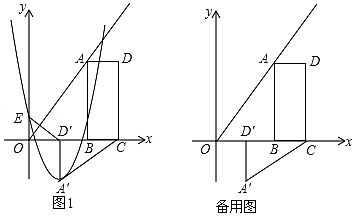
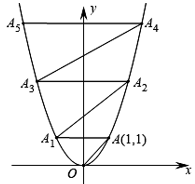
①求a、
B、m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.