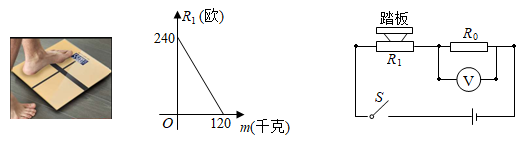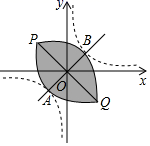

 B .
B . 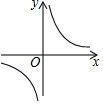 C .
C .  D .
D . 
近视眼镜的度数y(度) | 200 | 250 | 400 | 500 | 1000 |
镜片焦距x(米) | 0.50 | 0.40 | 0.25 | 0.20 | 0.10 |
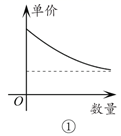
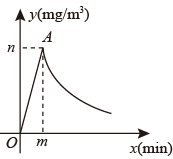



①求出当4≤x≤8时的函数关系式;
②求出当8<x≤28时的函数关系式.
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.