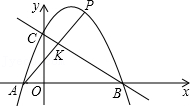



(Ⅰ)当 时,解答下列问题:
①求A点的坐标;
②连接 ,
,求
面积的最大值;
③当 的面积最大时,直线
也截得一个更小的抛物线弓形,同理在这个更小的抛物线弓形曲线上也有一点
,连接
,
,当
的面积最大时,求这个
的最大面积与②中
的最大面积的比值;
(Ⅱ)将(Ⅰ)中 的条件去掉后,其它条件不变,则
的最大面积与
的最大面积的比值是否变化?请说明理由.

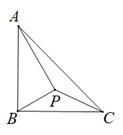
①求 的最大值;
②连接 ,当
与
相似时,求点P的坐标.


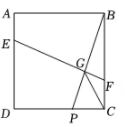
①求∠CDE的取值范围;
②如图2,取DE的中点G,连接CG并延长交直线DF于点H,点P为正方形内一动点,试求PH+PA+PB的最小值.