初中数学浙教版八下数学综合题优生特训3-在线组卷

1. (2022八下·新昌期中) 某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图：

（1）根据上图求出下表所缺数据

	平均数	中位数	众数	方差
甲班	8.5	8.5
乙班		8	10	1.6

（2）根据上表中的平均数和方差，你认为哪班的成绩较好？并说明你的理由．

答案解析收藏纠错 + 选题

2. (2022八下·义乌期中) 为弘扬泰山文化，我市某校举办了“泰山诗文大赛”活动，小学、初中部根据初赛成绩，各选出5名选手组成小学代表队和初中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如下图所示．

（1）根据图示填写图表；

	平均数（分）	中位数（分）	众数（分）
小学部		85
初中部	85		100

（2）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．

答案解析收藏纠错 + 选题

3. (2022八下·北仑期中) 为喜庆建党百年华诞，某校选拔一名选手参加我区“庆建党百年，忆红色初心”主题演讲比赛，经研究，按各项目得分情况对选拔赛参赛选手进行考评.下列是入围选手李明、张华在选拔赛中各项目的得分情况和各项目在总分中所占比率的扇形图：

项目

选手

服装

普通话

主题

演讲技巧

李明

85

70

80

85

张华

90

75

80

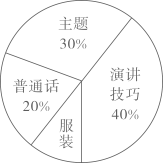
结合以上信息，回答下列问题：

（1）服装项目得分占总分的百分率是普通话项目对应扇形的圆心角大小是；
（2）李明在选拔赛中四个项目所得分数的众数是和中位数是；
（3）根据你所学的知识，帮助学校在李明、张华两人中选择一人参加“庆建党百年，忆红色初心”主题演讲比赛，并简要说明你的理由．

答案解析收藏纠错 + 选题

4. (2022八下·萧山期中) 某工艺品厂草编车间共有16名工人，调查每个工人的日均生产能力，获得数据如下表：

日均生产能力（件）	10	11	12	13	14	15
人数	1	3	5	4	2	1

（1）求这16名工人日均生产件数的平均数、众数、中位数．
（2）若以中位数作日生产件数的定额，求能完成任务的工人数占总人数的比值？

答案解析收藏纠错 + 选题

5. (2022八下·宁海期中) 浙江某大学部分专业采用“三位一体”的形式进行招生，现有甲、乙两名学生，他们各自的三类成绩（已折算成满分100分）如表所示：

学生	学业水平测试成绩	综合测试成绩	高考成绩
甲	85	89	81
乙	88	81	83

（1）如果根据三项得分的平均数，那么哪位同学排名靠前？
（2） “三位一体”根据入围考生志愿，按综合成绩从高分到低分择优录取，综合成绩按“学业水平测试成绩×20%+综合测试成绩×20%+高考成绩×60%”计算形成，那么哪位同学排名靠前？

答案解析收藏纠错 + 选题

6. (2022八下·温州期中) 某车间有工人10人，某月他们生产的零件个数统计如下表：

生产零件的个数（个）	600	480	220	180	120
工人人数（人）	1	1	3	4	1

（1）求这10名工人该月生产零件的平均个数；
（2）为了调动工人的积极性，决定实行目标管理，对完成目标的工人进行适当的奖励．如果想让一半左右的工人都能获得奖励，请你从平均数、中位数、众数的角度进行分析，该如何确定月生产目标？

答案解析收藏纠错 + 选题

7. (2022八下·富阳期中) 在开展“学雷锋社会实践”活动中某校为了了解全校2000名学生参加活动的情况，随机调查了40名学生每人参加活动的次数，并根据数据绘成条形统计图如图：

（1）这40．名学生每人参加活动的次数的众数是次，中位数是次．
（2）列式求这40名学生每人参加活动次数的平均数．

答案解析收藏纠错 + 选题

8. (2022八下·龙港期中) 某校八年级段进行跳远测试，学生的成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为10分，9分，8分，7分．小民将八年（1）班和八年（2）班的成绩整理并绘制成统计图如图所示．

请你根据所提供的信息解答下列问题：

（1）将表格补充完整．

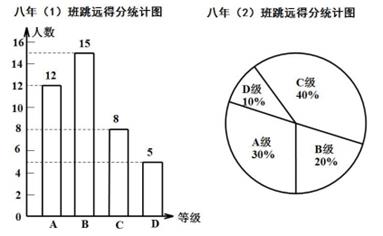
班级	平均数（分）	中位数（分）	众数（分）
八年（1）班	8.85		9
八年（2）班		8.5

（2）请结合平均数、中位数、众数等统计量进行分析，你认为哪个班级的成绩更好?并简述理由．

答案解析收藏纠错 + 选题

9. (2022八下·鄞州期中) 疫情防控已成为常态化，为了解学生对疫情防控措施的知晓情况，某校保健室开展了“疫情防控知识”问卷测试（满分10分）．他们将全校学生成绒进行统计，并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图（不完整）．

组号	成绩	频数	频率
1	$\text{[math]}$	2	0.050
2	$\text{[math]}$	6	0.150
3	$\text{[math]}$	a	0.450
4	$\text{[math]}$	9	0.225
5	$\text{[math]}$	b	m
6	$\text{[math]}$	2	0.050
	合计	40	1.000

根据以上提供的信息，解答下列问题：

（1）表格中 $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ；补全频数分布直方图；
（2）这40位同学成绩的中位数落在哪一个小组？
（3）全校共有1200位同学参与测试，若以组中值（每组成绩的中间数值）为本组数据的代表，请估计所有同学成绩的平均分大约是多少？

答案解析收藏纠错 + 选题

10. (2022八下·遂昌期中) 某校八年级开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间每人踢100个以上（含100个）为优秀，下列是成绩最好的甲班和乙班5名学生的比赛数据（单位：个），

	1号	2号	3号	4号	5号	总分
甲班	100	98	110	89	103	500
乙班	86	100	98	119	97	500

经统计发现两班总分相等，此时有学生建议，可通过考查数据中的其他信息作为参考，请你回答下列问题：

（1）计算甲、乙两班的优秀率.
（2）求两班比赛成绩的中位数.
（3）计算两个比赛数据的方差.
（4）根据以上信息，你认为应该把冠军奖状发给哪一个班级？简述你的理由.

答案解析收藏纠错 + 选题

11. (2022八下·温州期中) 国家实施“双减”政策后，学生学业负担有所减轻，很多家长选择利用周末时间带孩子去景区游玩．某调查小组从去过乐清雁荡山和江心屿的学生中各随机抽取了20名学生对这两个景区分别进行评分(满分10分)，并通过整理和分析，给出了部分信息．

乐清雁荡山景区得分情况：

7，8，7，10，7，6，9，9，10，10，8，9，8，6，6，10，9，7，9，9．

江心屿得分情况：

7，8，7，6，7，6，9，9，10，10，8，8，8，6，6，10，8，7，8，8．

抽取的学生对两个景区分别打分的平均数、众数和中位数如下表．

	平均数	众数	中位数
乐清雁荡山	8.2	9	b
江心屿	7.8	a	8

根据以上信息，解答下列问题：

（1）直接写出上述图表中的a，b的值a=，b=
（2）根据上述数据，你认为去过这两个景区的学生对哪个景区评价更高？请说明理由(写出一条理由即可)．

答案解析收藏纠错 + 选题

12. (2022八下·长兴期中) 某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额(单位：万元)，并根据统计的这组销售额数据，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：

（1）该商场服装部营业员的人数为，图①中m的值为；
（2）求统计的这组销售额数据的平均数、众数和中位数．

答案解析收藏纠错 + 选题

13. (2022八下·厦门期中) 小宇观看奥运会跳水比赛，对运动员每一跳成绩的计算方法产生了浓厚的兴趣，查阅资料后，小宇了解到跳水比赛的计分规则为：

a.每次试跳的动作，按照其完成难度的不同，对应一个难度系数H；

b.每次试跳都有7名裁判进行打分（0~10分，分数为0.5的整数倍），在7个得分中去掉2个最高分和两个最低分，剩下3个得分的平均值为这次试跳的完成分p；

c.运动员该次试跳的得分A＝难度系数H×完成分p×3.

在比赛中，甲运动员最后一次试跳后的打分表为：

难度系数	裁判	1#	2#	3#	4#	5#	6#	7#
3.5	打分	7.5	8.5	4.0	9.0	8.0	8.5	7.0

（1）甲运动员这次试跳的完成分P_甲＝，得分A_甲＝；（直接写出答案）
（2）若按照全部7名裁判打分的平均分来计算完成分，得到的完成分为P_甲_' ，那么与（1）中所得的P_甲比较，判断P_甲_' ▲ P_甲（填“＞”，“＝”或“＜”）并说明理由；
（3）在最后一次试跳之前，乙运动员的总分比甲运动员低13.1分，乙最后一次试跳的难度系数为3.6，若乙想要在总分上反超甲，则这一跳乙的完成分P乙至少要达到多少分.

答案解析收藏纠错 + 选题

14. (2022八下·杭州月考) 农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位：cm）进行了测量。根据统计的结果，绘制出如下的统计图①和图②.

请根据相关信息，解答下列问题：

（1）本次抽取的麦苗的株树为，图①中m的值为．
（2）求统计的这组苗高数据的平均数、众数和中位数.

答案解析收藏纠错 + 选题

15. (2022八下·拱墅月考) 为庆祝中国共产党建党100周年，某中学组织七、八年级全体学生开展了“党史知识”竞赛活动，为了解竞赛情况，从两个年级各抽取10名学生的成绩 ( 满分为100分 ) .
收集数据：
七年级： 90、95、95、80、85、90、80、90、85、100 ；
八年级：85、85、95、80、95、90、90、90、100、90.

分析数据：

	平均数	中位数	众数	方差
七年级	89	$\text{[math]}$	90	39
八年级	$\text{[math]}$	90	$\text{[math]}$	$\text{[math]}$

根据以上信息回答下列问题：

（1）请直接写出表格中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值；
（2）通过计算求出 $\text{[math]}$ 的值；
（3）通过数据分析，你认为哪个年级的成绩比较好？说明理由；

答案解析收藏纠错 + 选题

16. (2022八下·乐清月考) 某中学举行“中国梦”校园好声音歌手比赛，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，根据这10人的决赛成绩（满分为100分），制作了如图统计图：

（1）根据上图提供的数据填空：

	平均数	中位数	众数	方差
初中部	*	85	b	70
高中部	85	a	100	*

a的值是，b的值是；

（2）结合两队的平均数和中位数，分析哪个队的决赛成绩好；
（3）根据题（1）中的数据，试通过计算说明，哪个代表队的成绩比较稳定？

答案解析收藏纠错 + 选题

17. (2021八下·新市区期末) 我市某中学举办“网络安全知识竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示：

	平均分（分）	中位数（分）	众数（分）	方差
初中部	a	85	b	$\text{[math]}$
高中部	85	c	100	160

（1）根据图示求出a，b，c的值；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算初中代表队决赛成绩的方差 $\text{[math]}$ ，并判断哪一个代表队选手成绩较为稳定.

答案解析收藏纠错 + 选题

18. (2021八下·沙坪坝期末) 在第26个“世界读书日”来临之际，某学校开展了“书香满校园，阅读伴成长”的阅读知识竞赛活动，为了解竞赛情况，随机抽取了20名学生的成绩（竞赛成绩均为整数，满分10分），成绩如下：6，5，8，7，10，7，9，8，4，7，10，6，8，9，7，8，5，8，6，10

整理数据：

分数	4	5	6	7	8	9	10
学生人数	1	a	3	4	b	2	3

根据以上信息回答下列问题：

（1）填空：a＝，b＝；
（2）请求出这20名学生成绩的平均数和中位数；
（3）抽取的20名学生中，小明的成绩为8分，你认为小明的成绩在抽取的20名学生的成绩中属于“中上”水平吗？请说明理由.

答案解析收藏纠错 + 选题

19. (2021八下·綦江期末) 电影《你好，李焕英》成为今年春节电影档的黑马，截至2021年3月17日票房已达52.78亿．为了解大家对这部电影的喜爱程度，小李3月17日在 $\text{[math]}$ 重影綦江影院、綦江万达广场 $\text{[math]}$ 店观看这部电影的观众中，各抽取了 $\text{[math]}$ 名观众，统计这部分观众对电影的评价分效（满分10分，用 $\text{[math]}$ 表示评价分数，共分为 $\text{[math]}$ 组：A： $\text{[math]}$ ；B： $\text{[math]}$ ；C： $\text{[math]}$ ；D： $\text{[math]}$ ；），并对数据进行整理、描述和分析，下面给出了部分信息．

其中CFG重影綦江影院观众的评分位于 $\text{[math]}$ 组有14人，评分分别为：9.2，9.2，9.2，

9.2，9.3，9.5，9.5，9.6，9.6，9.7 ， 9.8，9.8，10，10 ；

两家电影院观众评分的平均数，中位数，众数（单位：分）如表所示：

电影院	$\text{[math]}$ 重影綦江影院	綦江万达广场 $\text{[math]}$ 店
平均数	9.2	9.2
中位数	$\text{[math]}$	9.5
众数	9.2	9.5

（1）填空： $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ，并补全条形统计图；
（2）通过以上数据分析，你认为哪个电影院的观众更喜欢这部电影？请说明理由（一条理由即可）；
（3） 3月17日， $\text{[math]}$ 重影綦江影院、綦江万达广场 $\text{[math]}$ 店共有600人观看这部电影，请估计这600人中给出这部电影评分高于9分的观众人数是多少？

答案解析收藏纠错 + 选题

20. (2021八下·宁波期末) 博才中学要从甲、乙两名同学中选拔一名同学代表学校参加“华罗庚金杯”数学竞赛活动.这两位活动同学最近四次的数学测验成绩如下表：（单位：分）

	第一次	第二次	第三次	第四次
甲	75	70	85	90
乙	85	82	75	78

（1）根据表中数据，分别求出甲、乙两名同学这四次数学测验成绩的平均分.
（2）经计算，甲、乙两位同学这四次数学测验成绩的方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，你认为哪位同学的成绩较稳定?请说明理由.

答案解析收藏纠错 + 选题

21. (2021九上·亭湖月考) 某篮球队对队员进行定点投篮测试，每人每次投篮10次，现对甲、乙两名队员在五次中进球数（单位：个）进行统计，结果如表：

	第1次	第2次	第3次	第4次	第5次
甲	10	6	10	6	8
乙	7	9	7	8	9

经过计算，甲进球的平均数为8，方差为3.2.

（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？

答案解析收藏纠错 + 选题

22. (2021八下·江干期末) 某学校从九年级同学中任意选取20人进行“引体向上”体能测试，前后进行了两次测试，第一次测试绘制成统计图，第二次测试绘制成统计表.

成绩	7	8	9	10
人数	1	5	10	4

（1） m＝，第一次测试成绩的中位数是，第二次测试成绩的众数是；
（2）请计算第一次测试的平均成绩；
（3）若9分及以上为优秀，请计算两次测试中优秀人数增加的百分比（精确到0.1%）.

答案解析收藏纠错 + 选题

23. (2021八下·滨江期末) 甲、乙二人加工同一批零件，零件内径合格尺寸是（单位：毫米）：297≤ΦD≤302.质检员分别从二人各自加工的100个零件中随机抽取5个

甲：302，299，296，299，299；

乙：300，298，297，300，300.

（1）完成如表：

平均数

中位数

众数

方差

甲

299

299

乙

299

300

$\text{[math]}$
（2）根据以上信息，你认为如何评价两人的加工质量？

答案解析收藏纠错 + 选题

24. (2021八下·南陵期末) “新型冠状病毒肺炎”疫情牵动着亿万国人的心，为进一步加强疫情防控工作，某校利用网络平台进行疫情防控知识测试，测试题共10小题，每小题10分.小明同学对八（1）班和八（2）班两个班各40名同学的测试成绩（单位：分）进行了整理和分析，统计数据如下：

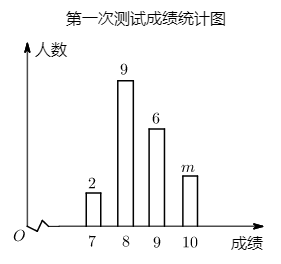
①八（1）班成绩频数分布直方图如图：

②八（2）班成绩平均分的计算过程如下：

$\text{[math]}$ （分）；

③数据分析如下：

班级	平均数	中位数	众数	方差
八（1）班	82.5	$\text{[math]}$	90	158.75
八（2）班	80.5	75	$\text{[math]}$	174.75

根据以上信息，解答下列问题：

（1） $\text{[math]}$ ， $\text{[math]}$ ；
（2）你认为班的成绩更加稳定，理由是；
（3）在本次测试中，八（1）班甲同学和八（2）班乙同学的成绩均为80分，你认为两人在各自班级中谁的成绩排名更靠前?请说明理由.

答案解析收藏纠错 + 选题

25. (2021八下·江北期末) 某校八年级两个班，各选派10名学生参加学校举行的“汉字听写大赛”预赛，各参赛选手的成绩如下：

八（1）班：91，92，93，93，93，94，98，88，98，100

八（2）班：93，93，93，95，96，96，98，89；98，99

通过整理，得到数据分析表如下：

班级	最高分	平均分	中位数	众数	方差
八（1）班	100	$\text{[math]}$	93	93	12
八（2）班	99	95	$\text{[math]}$	$\text{[math]}$	8.4

（1）直接写出表中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值；
（2）依据数据分析表，有人说：“八（1）班的最高分100大于八（2）班的最高分99，八（1）班的成绩比八（2）班好”，但也有人说八（2）班的成绩比较好，请给出两条支持八（2）班成绩好的理由.

答案解析收藏纠错 + 选题

26. (2021八下·舞阳期末) 为加强抗击疫情的教育宣传，某中学开展防疫知识线上竞赛活动，八年级（1）、（2）班各选出5名选手参加竞赛，两个班各选出的 $\text{[math]}$ 名选手的竞赛成绩（满分为 $\text{[math]}$ 分）如图所示：

（1）请你计算两个班的平均成绩各是多少分；
（2）写出两个班竞赛成绩的中位数，结合两个班竞赛成绩的平均数和中位数，你认为哪个班的竞赛成绩较好；
（3）计算两个班竞赛成绩的方差，并说明哪个班的竞赛成绩较为整齐.

答案解析收藏纠错 + 选题

27. (2021八下·鄞州期末) 据悉某市即将建设海上风电项目，需要铺设一条海底电缆，项目方从甲、乙两厂中分别选取6根不同批次的电缆检测载流量，数据统计如下（抽样数据单位：千安）.

甲、乙两厂电缆载流量统计表

电缆	一	二	三	四	五	六	平均数	中位数	众数	方差
甲厂	1.6	1.6	1.3	0.7	1.3	1.3	a	1.3	1.3	0.09
乙厂	0.7	1.5	1.5	1.3	1.5	1.3	1.3	b	c	0.08

（1）补全表中数据， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
（2）若优质的电缆是有较高的载流量且性能稳定，请你结合表中数据，帮助项目方选择合适的电缆厂家，并写出两条推荐理由.

答案解析收藏纠错 + 选题

28. (2021八下·西湖期末) 某区要举办中学生科普知识竞赛，我校要选拔一支代表队参赛.选拔赛满分为100分，规定85分及以上为“合格”，95分及以上为“优秀”.现将A，B两支预选队的竞赛成绩统计如下：

组别	$\text{[math]}$ 队	$\text{[math]}$ 队
平均分	88	87
中位数	90	a
方差	61	71
合格率	70%	b
优秀率	30%	25%

（1）求出表中a，b的值
（2）若从A，B两队中选取成绩前20名（包括第20名）的学生组成代表队，小明的成绩正好是本队成绩的中位数，但他却落选了，那么小明应属于哪个队？请说明理由.

答案解析收藏纠错 + 选题

29. (2021八下·睢县期末) 甲、乙两人在“定位投篮”选拔赛测试中（共10轮，每轮投10个球）成绩如下：

（1）填表：

平均数

中位数

众数

方差

甲

7.5

8

乙

7

1.2
（2）如果你是教练，你会选择谁参加正式比赛？请说明理由.

答案解析收藏纠错 + 选题

30. (2021八下·梁园期末) 随着信息技术的高速发展，计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣，老师把甲、乙两组各有10名学生，进行电脑汉字输人速度比赛，各组参赛学生每分钟输入汉字个数统计如下表：

输入汉字（个）	132	133	134	135	136	137
甲组人数（人）	1	0	1	5	2	1
乙组人数（人）	0	1	4	1	2	2

（1）请你填写下表中甲班同学的相关数据.

组别	众数	中位数	平均数（ $\text{[math]}$ ）	方差（ $\text{[math]}$ ）
甲组人数（人）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1.6
乙组人数（人）	134	134.5	135	1.8

则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

（2）若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？
（3）请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）

答案解析收藏纠错 + 选题

小学

初中

高中

初中数学浙教版八下数学综合题优生特训3

副标题：

*注意事项：

初中数学浙教版八下数学综合题优生特训3

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析