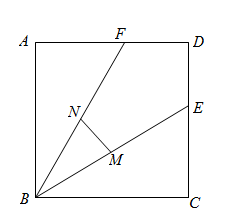




梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中,
, 四边形
、
和
分别是以
的三边为一边的正方形.延长
和
, 交于点
, 连接
并延长交
于点
, 交
于点
, 延长
交
于点
.
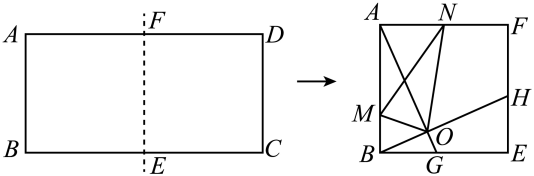
如图2,四边形和
分别是以
的两边为一边的平行四边形,探索在
下方是否存在平行四边形
, 使得该平行四边形的面积等于平行四边形
、
的面积之和.若存在,作出满足条件的平行四边形
(保留适当的作图痕迹);若不存在,请说明理由.


