浙教版备考2023年中考数学一轮复习82.解直角三角形及其应...

更新时间：2023-01-01 浏览次数：163 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2023·宽城模拟) 如图，一条河两岸互相平行，为测得此河的宽度PT（PT与河岸PQ垂直），测P、Q两点距离为m米， $\text{[math]}$ ，则河宽PT的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·长春) 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图，该起重机的变幅索顶端记为点A，变幅索的底端记为点B， $\text{[math]}$ 垂直地面，垂足为点D， $\text{[math]}$ ，垂足为点C．设 $\text{[math]}$ ，下列关系式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·牟平期中) 数学活动小组到某广场测量标志性建筑AB的高度．如图，他们在地面上C点测得最高点A的仰角为22°，再向前70m至D点，又测得最高点A的仰角为58°，点C，D，B在同一直线上，则该建筑物AB的高度约为（）（精确到1m．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

A . 28m B . 34m C . 37m D . 46m

答案解析收藏纠错 + 选题
4. (2022·毕节) 如图，某地修建一座高 $\text{[math]}$ 的天桥，已知天桥斜面 $\text{[math]}$ 的坡度为 $\text{[math]}$ ，则斜坡 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·黔东南) 如图，已知正六边形 $\text{[math]}$ 内接于半径为 $\text{[math]}$ 的 $\text{[math]}$ ，随机地往 $\text{[math]}$ 内投一粒米，落在正六边形内的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 以上答案都不对

答案解析收藏纠错 + 选题
6. (2023九上·郑州经济技术开发月考) 如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·德城模拟) 如图，已知△ABC内接于半径为1的⊙O，∠BAC=θ（θ是锐角），则△ABC的面积的最大值为（）

A . cosθ(1+cosθ) B . cosθ(1+sinθ) C . sinθ(1+sinθ) D . sinθ(1+cosθ)

答案解析收藏纠错 + 选题
8. 如图，一轮船以16海里 $\text{[math]}$ 时的速度从港口 $\text{[math]}$ 出发向东北方向航行，另一轮船以12海里 $\text{[math]}$ 时的速度同时从港口 $\text{[math]}$ 出发向东南方向航行，离开港口2小时后，两船相距（）

A . 40海里 B . 35海里 C . $\text{[math]}$ 海里 D . 25海里

答案解析收藏纠错 + 选题
9. (2022·安次模拟) 如图，洋洋一家驾车从A地出发，沿着北偏东60°的方向行驶，到达B地后沿着南偏东50°的方向行驶来到C地，且C地恰好位于A地正东方向，则下列说法正确的是（）

A . B地在C地的北偏西40°方向上 B . A地在B地的南偏西30°方向上 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·龙港模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是正方形 $\text{[math]}$ 边上的线段，点 $\text{[math]}$ 在其中某条线段上，若射线 $\text{[math]}$ 与 $\text{[math]}$ 轴正半轴的夹角为 $\text{[math]}$ ，且 $\text{[math]}$ ，则点 $\text{[math]}$ 所在的线段可以是 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ 和 $\text{[math]}$ B . $\text{[math]}$ 和 $\text{[math]}$ C . $\text{[math]}$ 和 $\text{[math]}$ D . $\text{[math]}$ 和 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每空3分，共24分）

11. (2022九上·舟山月考) 小明沿着坡比为1：2的山坡向上走了10m，则他升高了cm。

答案解析收藏纠错 + 选题
12. (2022·黔西) 如图，我海军舰艇在某海域C岛附近巡航，计划从A岛向北偏东80°方向的B岛直线行驶．测得C岛在A岛的北偏东50°方向，在B岛的北偏西40°方向．A，B之间的距离为80nmile，则C岛到航线AB的最短距离是nmile．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ，保留整数结果）

答案解析收藏纠错 + 选题
13. (2022·柳州) 如图，某水库堤坝横断面迎水坡的坡角为 $\text{[math]}$ ， $\text{[math]}$ ，堤坝高 $\text{[math]}$ ，则迎水坡面 $\text{[math]}$ 的长度为 $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2022·烟台) 如图1，△ABC中，∠ABC＝60°，D是BC边上的一个动点（不与点B，C重合），DE $\text{[math]}$ AB，交AC于点E，EF $\text{[math]}$ BC，交AB于点F．设BD的长为x，四边形BDEF的面积为y，y与x的函数图象是如图2所示的一段抛物线，其顶点P的坐标为（2，3），则AB的长为．

答案解析收藏纠错 + 选题
15. (2022·宁夏) 2022年4月16日9时56分，神舟十三号载人飞船返回舱在东风着陆场成功着陆，某一时刻观测点D测得返回舱底部C的仰角∠CDE＝45°，降落伞底面圆A点处的仰角∠ADE＝46°12′．已知半径OA长14米，拉绳AB长50米，返回舱高度BC为2米，这时返回舱底部离地面的高度CE约为米（精确到 $\text{[math]}$ 米）．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
16. (2022九上·蚌埠月考) 如图，将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下，使木桩向上移动．已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm（如箭头所示），则木桩上升了 .（结果可含有三角函数）

答案解析收藏纠错 + 选题
17. (2022八上·东阳期中) 如图1是吊车的实物图，图2是吊车工作示意图，车顶BM与车身CN平行于地面，已知BM到地面的距离为2米，AD＝4.8米，∠MBC＝3∠BCN.吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的，从而使得起重臂升降作业.在某次起重作业中，学习兴趣小组经过测量发现：液压杆CD为2米时，∠DCN＝120°，∠MBD＝150°，则∠CBD＝度，此时点A到地面的距离为米.

答案解析收藏纠错 + 选题

三、作图题（共8分）

18. (2022·道外模拟) 如图，网格中的每个小正方形的边长均为1，线段AB的端点均在小正方形的顶点上．
⑴在图中画出以AB为一边的菱形ABCD，点C和点D在小正方形顶点上；
⑵在图中画出以AB为斜边的直角三角形ABE，点E在小正方形顶点上，且 $\text{[math]}$ ，连接CE，请直接写出线段CE的长．

答案解析收藏纠错 + 选题

四、综合题（共7题，共58分）

19. (2023·冠县模拟) 如图，湖边 $\text{[math]}$ 、 $\text{[math]}$ 两点由两段笔直的观景栈道 $\text{[math]}$ 和 $\text{[math]}$ 相连.为了计算 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离，经测量得： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 米，求 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2022·徐州) 如图，公园内有一个垂直于地面的立柱AB，其旁边有一个坡面 $\text{[math]}$ ，坡角 $\text{[math]}$ ．在阳光下，小明观察到在地面上的影长为 $\text{[math]}$ ，在坡面上的影长为 $\text{[math]}$ ．同一时刻，小明测得直立于地面长60cm的木杆的影长为90cm（其影子完全落在地面上）．求立柱AB的高度．

答案解析收藏纠错 + 选题
21. (2022·攀枝花) 第24届冬奥会（也称2022年北京冬奥会）于2022年2月4日至2月20日在中国北京举行，北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆，整个动作连贯一致，一气呵成，如图，某运动员穿着滑雪板，经过助滑后，从倾斜角 $\text{[math]}$ 的跳台A点以速度 $\text{[math]}$ 沿水平方向跳出，若忽略空气阻力影响，水平方向速度将保持不变.同时，由于受重力作用，运动员沿竖直方向会加速下落，因此，运动员在空中飞行的路线是抛物线的一部分，已知该运动员在B点着陆， $\text{[math]}$ ，且 $\text{[math]}$ .忽略空气阻力，请回答下列问题：
1. （1）求该运动员从跳出到着陆垂直下降了多少m？
2. （2）以A为坐标原点建立直角坐标系，求该抛物线表达式；
3. （3）若该运动员在空中共飞行了4s，求他飞行2s后，垂直下降了多少m？
答案解析收藏纠错 + 选题
22. (2022·大连) 如图，莲花山是大连著名的景点之一，游客可以从山底乘坐索道车到达山项，索速车运行的速度是1米/秒，小明要测量莲花山山顶白塔的高度，他在索道A处测得白塔底部B的仰角的为 $\text{[math]}$ ，测得白塔顶部C的仰角的为 $\text{[math]}$ ．索道车从A处运行到B处所用时间的为5分钟．
1. （1）索道车从A处运行到B处的距离约为米；
2. （2）请你利用小明测量的数据，求白塔 $\text{[math]}$ 的高度（结果取整数）．（参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
23. (2022九上·舟山月考) 购物广场要修建一个地下停车场，停车场的入口设计示意图如图所示，其中斜坡的倾斜角为18°，一楼到地下停车场地面的垂直高度CD＝2.8m，一楼到地平线的距离BC=1m.
1. （1）为保证斜坡的倾斜角为18°，应在地面上距点B多远的A处开始斜坡的施工？（结果精确到0.1m）
2. （2）如果给该购物广场送货的货车高度为2.5m，那么按这样的设计能否保证货车顺利进入地下停车场？并说明理由．（参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）
答案解析收藏纠错 + 选题
24. (2022·重庆) 如图，在锐角△ABC中，∠A=60°，点D，E分别是边AB，AC上一动点，连接BE交直线CD于点F．
1. （1）如图1，若AB>AC，且BD=CE，∠BCD=∠CBE，求∠CFE的度数；
2. （2）如图2，若AB=AC，且BD=AE，在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM，连接MF，点N是MF的中点，连接CN．在点D，E运动过程中，猜想线段BF，CF，CN之间存在的数量关系，并证明你的猜想；
3. （3）若AB=AC，且BD=AE，将△ABC沿直线AB翻折至△ABC所在平面内得到△ABP，点H是AP的中点，点K是线段PF上一点，将△PHK沿直线HK翻折至△PHK所在平面内得到△QHK，连接PQ．在点D，E运动过程中，当线段PF取得最小值，且QK⊥PF时，请直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
25. (2022·榆次模拟) 综合与实践
问题背景：
在综合与实践课上，老师让同学们探索有一组邻边相等，一组对角互补的四边形的性质．如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）实践操作：
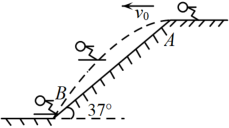
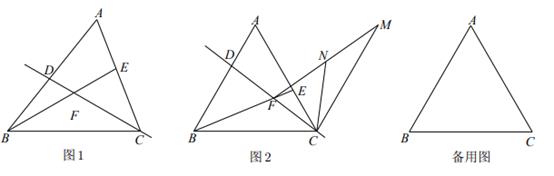
  同学们首先从特殊情形开始探索，如图2，当 $\text{[math]}$ 时，其它条件不变，发现了 $\text{[math]}$ 平分 $\text{[math]}$ 的性质，有两个小组给出如下的证明思路：
  “团结组”：利用“在一个角的内部，到角的两边距离相等的点在这个角的平分线上”；
  “实践组”：由 $\text{[math]}$ 想到将 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，将四边形 $\text{[math]}$ 转化成我们学过的特殊图形．
  ①请你分别在图2，图3中画出符合“团结组”和“实践组”思路的辅助线；
  ②求证： $\text{[math]}$ 平分 $\text{[math]}$ ；（从上面的两个思路中选一个或按照自己的思路）
2. （2） “创新组”的同学发现在图2中 $\text{[math]}$ ，请你说明理由；
3. （3）拓展延伸：
  “善思组”的同学受“创新组”同学的启发，提出如下问题：如图4，当 $\text{[math]}$ 时，其它条件不变，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，过点 $\text{[math]}$ 分别作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的形状为，四边形 $\text{[math]}$ 的面积为．
答案解析收藏纠错 + 选题