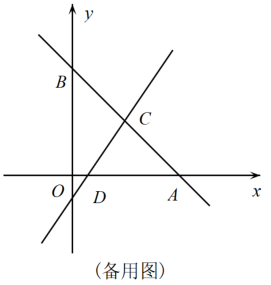
 B .
B .  C .
C .  D .
D . 
①∴ ,这与三角形内角和为
矛盾②因此假设不成立.∴
③假设在
中,
④由
,得
,即
.
这四个步骤正确的顺序应是( )



( 1 )在图①中,画等腰△ABC,使AB为腰,点C在格点上.
( 2 )在图②中,画面积为8的四边形ABCD,使其为中心对称图形,但不是轴对称图形,C,D两点均在格点上.
( 3 )在图③中,画△ABC,使∠ACB=90°,面积为5,点C在格点上.
【动手操作】小明同学在探究证明中位线性质定理时,是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形,从而得出:三角形中位线平行于第三边且等于第三边的一半.
【性质证明】小明为证明定理,他想利用三角形全等、平行四边形的性质来证明.请你帮他完成解题过程(要求:画出图形,根据图形写出已知、求证和证明过程).
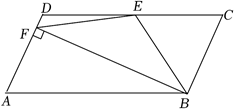
如图,在四边形ABCD中,E、F、G、H是各边中点,对角线AC、BD相交于点O,I、J是AC、BD的中点,连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1:四边形EFGH是平行四边形;
结论2:四边形EJGI是平行四边形;
结论3:;
……


①如图1,在四边形ABCD中,F、H分别为边AB,DC的中点,连结HF.已知 ,
, 线段HF的取值范围是 ▲ .
②如图2,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,连接EG,FH交于点O,cm,
cm,
, 求
.

①求证:四边形ABDE为平行四边形。
②求点A的坐标。