浙教版数学八年级下学期期末复习常考题微专练：正方形

更新时间：2023-05-13 浏览次数：67 类型：复习试卷

一、单选题（每题3分，共30分）

1. 顺次连结四边形ABCD各边中点所围成的四边形是正方形，则四边形ABCD的对角线（）

A . 互相垂直 B . 互相平分 C . 相等 D . 互相垂直且相等

答案解析收藏纠错 + 选题
2. (2024八下·义乌月考) 如图，矩形内有两个相邻的白色正方形，其面积分别为2和18，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 6

答案解析收藏纠错 + 选题
3. (2022八下·江北期中) 下列四个命题中，真命题是（）

A . 对角线垂直且相等的四边形是菱形 B . 对角线互相垂直平分的四边形是正方形 C . 一组邻边相等的平行四边形是正方形 D . 对角线相等且互相平分的四边形是矩形

答案解析收藏纠错 + 选题
4. “方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 沿对角线 $\text{[math]}$ 方向平移 $\text{[math]}$ 得到正方形 $\text{[math]}$ ，形成一个“方胜”图案，则点 $\text{[math]}$ ， $\text{[math]}$ 之间的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·定海期末) 如图，四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·杭州期中) 如图，在正方形ABCD中，AB=8，F是对角线AC的中点，点G、E分别在AD、CD边上运动，且保持AG=DE．连接GE、GF、EF．在此运动变化的过程中，下列结论：①△GFE是等腰直角三角形；②四边形DGFE不可能为正方形，③GE长度的最小值为4 $\text{[math]}$ ；④四边形DGFE的面积保持不变；⑤△DGE面积的最大值为8．其中正确的结论是（）

A . ①②③ B . ①③④⑤ C . ①③④ D . ③④⑤

答案解析收藏纠错 + 选题
7. (2023八下·宁海期中) 如图是一个由4张直角三角形纸片和1张正方形纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为 $\text{[math]}$ ，则这个平行四边形的面积为（）

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
8. (2023八下·仙居期中) 如图1所示，正方形 $\text{[math]}$ 中，点E是边的中点，动点P从点A出发，在正方形的边上沿A→B→E的路线匀速运动到点E停止，设点P的运动路程为x， $\text{[math]}$ ，图2是点P运动时y随x变化关系的图像，根据图中的数据，可知点Q的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八下·新昌期末) 如图在边长为1的小正方形构成的5×4的网格中，定义：以网格中的格点为顶点的正方形叫做格点正方形．则图中完全包含“”的格点正方形最多能画（）

A . 13个 B . 16个 C . 19个 D . 21个

答案解析收藏纠错 + 选题
10. (2023八下·仙居期中) 勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入长方形内得到的， $\text{[math]}$ ，点D，E，F，G，H，I都在长方形 $\text{[math]}$ 的边上，则长方形 $\text{[math]}$ 的面积为（）

A . 420 B . 440 C . 430 D . 410

答案解析收藏纠错 + 选题

二、填空题（每空4分，懂28分）

11. (2022八下·柯桥期末) 有三个相邻正方形的边长分别为 1、2、3，两端的两个正方形都有两个顶点在大正方形的边上且组成的图形为轴对称图形，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
12. (2022八下·杭州期末) 如图，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为正方形 $\text{[math]}$ 四边中点，连结 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积是.

答案解析收藏纠错 + 选题
13. (2022八下·上城期末) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的点， $\text{[math]}$ ，连结 $\text{[math]}$ ，作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023八下·杭州期中) 如图，正方形ABCD的边长为2，G是对角线BD上一动点，GE⊥CD于点E，GF⊥BC于点F，连结EF．给出四种情况：

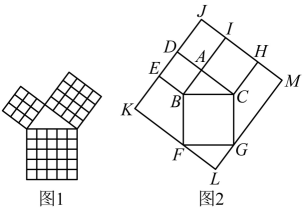
①若G为BD上任意一点，则AG=EF；

②若BG=AB，则∠DAG=22.5°；

③若G为BD的中点，则四边形CEGF是正方形；

④若DG：BG=1：3，则S_△_ADG= $\text{[math]}$

则其中正确的是.

答案解析收藏纠错 + 选题
15. (2023八下·义乌开学考) “勾股图”有着悠久的历史，欧几里得在《几何原本》中曾对它做了深入研究.如图，在△ABC中，∠ACB＝90°，分别以△ABC的三条边为边向外作正方形.连接EB，CM，DG，CM分别与AB，BE相交于点P，Q.若∠AMP＝30°，则∠ABE＝°， $\text{[math]}$ 的值为 .

答案解析收藏纠错 + 选题
16. (2022八下·南浔期末) 如图，已知在平面直角坐标系ｘＯｙ中，等腰直角三角形ABC的斜边AB⊥ｘ轴于点A，经过点B的反比例函数 $\text{[math]}$ （ｋ＞0，ｘ＞0）的图象交边AC于点D，连结ＯB，ＯC．若点D是AC中点，△ＯBC的面积为1，则ｋ的值是．

答案解析收藏纠错 + 选题

三、作图题（共6分）

17. (2022八下·柯桥期末) 图1，图2，图3，图4是四张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，A，C两点都在格点上，连结AC，请完成下列作图：
1. （1）以AC为对角线在图1中作一个正方形，且正方形各顶点均在格点上．
2. （2）以AC为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上．
3. （3）以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形（不含矩形），且平行四边形顶点在格点上.
答案解析收藏纠错 + 选题

四、综合题（共7题，共54分）

18. (2022九上·仙居开学考) 小明同学从一张面积为5的正方形Ⅰ中剪出一个面积为2的小正方形Ⅱ，并按如图所示摆放，其中A，B，C三点共线，求线段AD的长．

答案解析收藏纠错 + 选题
19. (2022八下·金东期末) 如图，正方形ABCD，边长为2，点E，F分别是AB，CD的中点，连结CE，AF，过点D作DG⊥AF，垂足为G，延长DG交CE于点H．
1. （1）求DG的长．
2. （2）求GH的长．
3. （3）求EH的长．
答案解析收藏纠错 + 选题
20. (2022八下·椒江期末) 如图，在正方形ABCD中，点E，F分别在边AD，CD上，且DE=CF，AF与BE相交于点G．
1. （1）求证：AF⊥BE；
2. （2）若AB=8，DE=2，求AG的长．
答案解析收藏纠错 + 选题
21. (2021八下·滨江期末) 如图，在正方形ABCD中，点E是对角线AC上一点，过点E作EF⊥AC，交边AD，AB于点F，H，连接CF，CH.
1. （1）求证：CF＝CH；
2. （2）若正方形ABCD的边长为1，当△AFH与△CDF的面积相等时，求AE的长.
答案解析收藏纠错 + 选题
22. (2022八下·定海期末) 在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上运动，点 $\text{[math]}$ 在边 $\text{[math]}$ 或 $\text{[math]}$ 上运动．
1. （1）若点 $\text{[math]}$ 在边 $\text{[math]}$ 上，
  $\text{[math]}$ 如图1，已知 $\text{[math]}$ ，连结 $\text{[math]}$ ，求证： $\text{[math]}$ ．
  $\text{[math]}$ 如图2，已知 $\text{[math]}$ 平分 $\text{[math]}$ ，求证： $\text{[math]}$ ．
2. （2）若点 $\text{[math]}$ 在边 $\text{[math]}$ 上，如图 $\text{[math]}$ ，已知 $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2022八下·临海期末) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点（不与端点 $\text{[math]}$ ， $\text{[math]}$ 重合），连接 $\text{[math]}$ 过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ≌ $\text{[math]}$ ；
2. （2） ①若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ；
  $\text{[math]}$ 改变 $\text{[math]}$ 的度数， $\text{[math]}$ 的度数是否会发生改变？若发生改变，请写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系，若不改变，请说明理由；
3. （3）如图2，若 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2022八下·舟山期末) 背景：点A在反比例函数y $\text{[math]}$ （k＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A在第一象限内，当AC＝4时，小李测得CD＝3．
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．
1. （1）求k的值．
2. （2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．
  ①求这个“Z函数”的表达式；
  
  ②补画x＜0时“Z函数”的图象；
  
  ③并写出这个函数的性质（两条即可）．
答案解析收藏纠错 + 选题