







①直角三角形两条直角边的平方和等于斜边的平方;
②等腰三角形两腰的高线相等;
③若三条线段a,b,c是三角形的三边,则这三条线段满足a+b>c
④角的内部,到角两边距离相等的点在这个角的平分线上,
⑤全等三角形的面积相等;





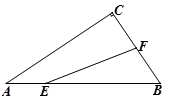
①如图2,若是
边上的任意一点,求证:
;
②若点是射线
上一点,
,
,
, 求
的长度.

思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在 上截取
,连接
,得到全等三角形,进而解决问题;
方法2:延长 到点N,使得
,连接
,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种 , 添加辅助线并完成证明.
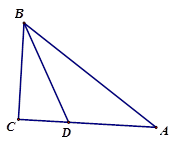
【探究方法】小强所在的小组通过探究发现,延长AD至点E,使ED=AD.连接BE,可以证出△ADC≌△EDB,利用全等三角形的性质可将已知的边长与AD转化到到△ABE中,进而求出AD的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线AD延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
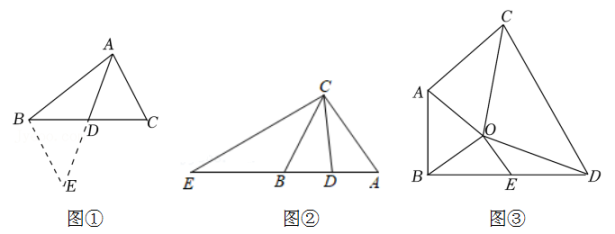
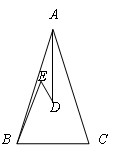
如图②,CB是△AEC的中线,CD是△ABC的中线,且AB=AC,下列四个选项中:
A.∠ACD=∠BCD B.CE=2CD C.∠BCD=∠BCE D.CD=CB
直接写出所有正确选项的序号是.
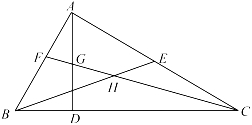
如图③,在△ABO和△CDO中,OA=OB,OC=OD,∠AOB与∠COD互补,连接AC、BD,E是BD的中点,求证:OE=AC.