B .
B .  C .
C .  D .
D . 
 B .
B . 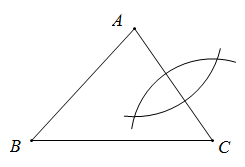 C .
C .  D .
D . 
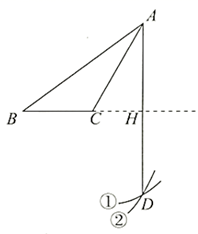
步骤1:以 为圆心,
长为半径画弧①;
步骤2:以 为圆心,
长为半径画弧②,交弧①于点
;
步骤3:连接 ,交
的延长线于点
.
则下列说法错误的是( )
已知:线段 ,
,小明用如图所示的方法作
,使
,
上的高
.
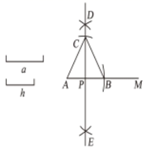
作法:①作射线 ,以点
为圆心、 ※ 为半径画弧,交射线
于点
;②分别以点
,
为圆心、 △ 为半径画弧,两弧交于点
,
;③作直线
,交
于点
;④以点
为圆心、
为半径在
上方画孤,交直线
于点
,连接
,
.
对于横线上符号代表的内容,下列说法错误的是( )
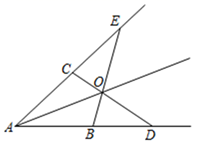
步骤1∶以C为圆心,CA为半径画弧①;
步骤2∶以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3∶连接AD,交BC延长线于点H.
下列叙述正确的是( )

|
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB作法:(1)以●为圆心,任意长为半径画弧,分别交OA、OB于点P、Q; (2)作射线EG,并以点E为圆心◎长为半径画弧交EG于点D; (3)以点D为圆心⊙长为半径画弧交(2)步中所画弧于点F; (4)作
|


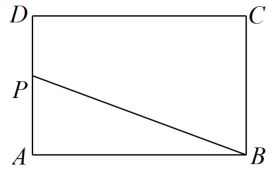
甲
连接
, 作
的中垂线分别交
、
于
点、
点,则
、
两点即为所求
乙
过
作与
平行的直线交
于
点,过
作与
平行的直线交
于
点,则
、
两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )

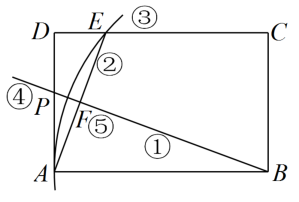


①两点确定一条直线;②两点之间线段最短;③垂线段最短.


①连接AB,点C在点B北偏东30°方向上,且BC=2AB,作出点C(保留作图痕迹);
②在(1)所作图中,D为BC的中点,连接AD,AC,画出∠ADC的角平分线DE交AC于点E;
③在①②所作图中,用量角器测量∠BDE的大小(精确到度).
下面是七年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)


因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
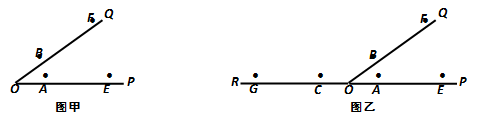
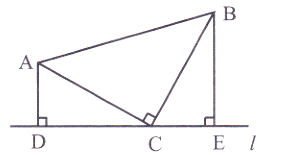
如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.
如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)

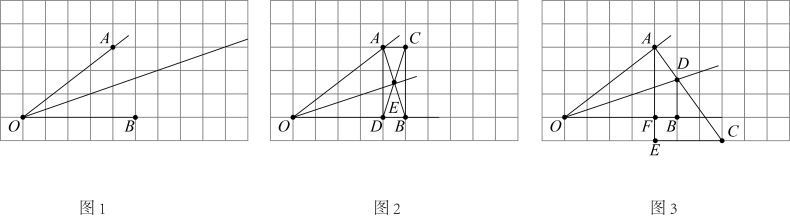
一次有意义的动手实践活动——在格点图中巧作角平分线
实践背景
在一次动手实践课上,老师提出如下问题:在如图1所示由边长为1的小正方形组成的格点图中,点 ,
,
都在小正方形的顶点处,仅用无刻度的直尺作出
的角平分线.
成果展示
小明、小亮展示了如下作法:
小明:如图2,在格点图中取格点 ,
. 连接
,
交于点
. 作出射线
.
∵四边形是矩形,∴
(依据1).
∵ , ∴
平分
.
小亮:如图3,在格点图中取格点 . 连接
, 与小正方形的边交于点
. 则
.
∵ ,
.
∴(依据2).
∴ , 即
平分
.
学习任务:
①请填写出上述材料中的依据1和依据2.
依据1: ▲ ;依据2: ▲ .
②请根据小亮的作法,证明 .
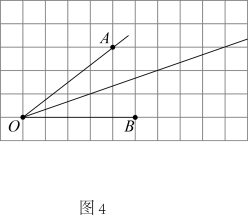
请你根据实践背景问题要求,采用不同于小明和小亮的作法,描出作图过程中的所取得的点,作出的角平分线(不写作法,不需要说明理由).
请在图中用直尺和圆规画出 的平分线
;(不写画法不需证明,保留作图痕迹)

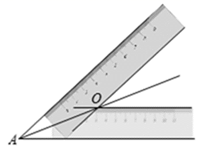
如图,将一把等宽直尺的一边依次落在 的两条边上,再过另一边分别画直线,两条直线相交于点O.画射线
,则射线
是
的平分线.这种角的平分线的画法依据的是______.
已知:如图,在 的两条边上分别画
,
,连接
、
,交点为点O,画射线
.
求证: 是
的平分线.