 B .
B . 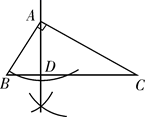 C .
C . 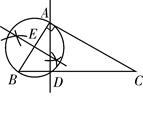 D .
D . 
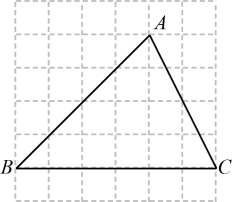
① ;
②当 时,
;
③当 时,四边形
是平行四边形;
④当 或
时,都有
;
⑤当 时,
与
一定相似.



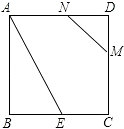




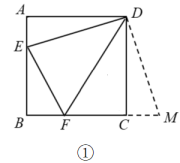
① 过点D作AB的平行线交BC于点F;
② P为AB边上的一点,且△DAP∽△PBC,请找出所有满足条件的点;

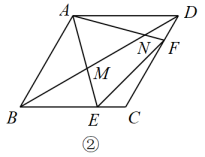
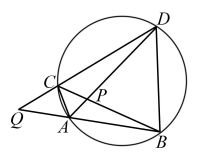
①当旋转至图2所示的位置时,求证:
;
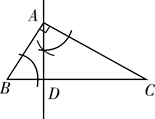
②如图3,当旋转至点D在
上时,
, 直接写出
及
的长.