






|
初步探索 |
素材1:
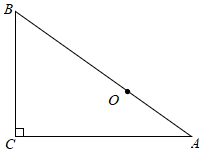
如图①,连接对应点 |
素材2:
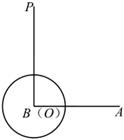
如图②,以 |
|
问题解决 |
(1)(ⅰ)请证明素材1所发现的结论. (ⅱ)如图2,过点
|
|
|
深入研究 |
(2)在 (ⅰ)如图③,当边 (ⅱ)若一时边 (3)在(2)的条件下,如图⑤,在旋转过程中,直线 |
|
如图2是旋转过程的一个位置,过点D作交
边于点E,连接
, 小明发现在三角板旋转的过程中,
度数是定值,求
的度数;
在(2)的条件下,设 ,
的面积为S,当
时,
①求的长;
②以点E为圆心,为半径作
, 并判断此时直线
与
的位置关系.