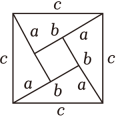
已知:如图,直线 ,
被直线
所截,
.
对说明理由.

方法 如图, |
方法 如图, |
下列说法正确的是( )

 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

证法1:如图, ∵∠A=70°,∠B=63°, 且∠ACD=133°(量角器测量所得) 又∵133°=70°+63°(计算所得) ∴∠ACD=∠A+∠B(等量代换). | 证法2:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质). |
下列说法正确的是( )

 B . 过AB上一点D作DE
B . 过AB上一点D作DE 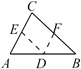 C . 延长AC到F,过C作CE
C . 延长AC到F,过C作CE  D . 作CD⊥AB于点D
D . 作CD⊥AB于点D 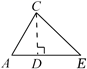
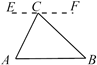
已知:如图,∠ACD是△ABC的外角.
求证:∠ACD=∠A+∠B.
证法1:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质)
证法2:如图,
∵∠A=88°,∠B=58°,
且∠ACD=146°(量角器测量所得)
又∵146°=88°+58°(计算所得)
∴∠ACD=∠A+∠B(等量代换)
下列说法正确的是( )

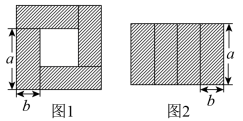
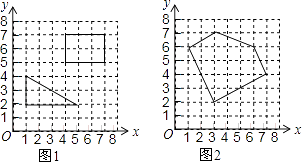
“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为S=a+ ﹣1,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是,并运用这个公式求得图2中多边形的面积是.
解析:的末尾数字等于
的末尾数字
∵ , 又
(n为正整数)的末尾数字均为6,
∴的末尾数字是
的末尾数字,即为8.
∴的末尾数字为8
根据以上阅读材料,回答下列问题:
.
①
②

验证:
②通过列式计算,说明新三位数与原三位数的差是9的倍数;


动手操作:在如图所示的平面直角坐标系中描出A,B,C三点,并连接 ,
;
观察发现:写出 ,
的中点坐标,观察中点坐标与线段两个端点的坐标,你能发现什么规律?
猜想验证:连接 , 直接写出
中点的坐标;
总结应用:已知点 ,
, 写出
中点的坐标.