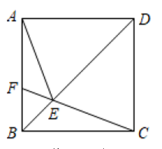
方案Ⅰ:如图1,先过点B作 , 再在
上取C,D两点,使
, 接着过点D作
的垂线
, 交
的延长线于点E,则测量
的长即可;
方案Ⅱ:如图2,过点B作 , 再由点D观测,用测角仪在
的延长线上取一点C,使
, 则测量
的长即可.
对于方案Ⅰ、Ⅱ,说法正确的是( )



已知:如图,钝角 . 求作:射线
, 使
.
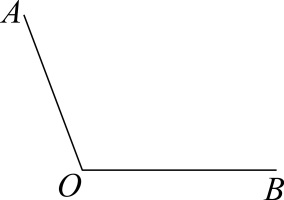
作法:
①在射线上任取一点
;
②以点为圆心,
长为半径作弧,交
于点
;
③分别以点为圆心,大于
长为半径作弧,在
内,两弧相交于点
;
④作射线 . 则
为所求作的射线.
证明:连接CD,CE,
由作图步骤②可知OD= ▲ ,
由作图步费③可知CD= ▲ ,
∵OC=OC,
∴△OCD≅△OCE.
∴∠AOC=∠BOC( )(填推理的依据).

