
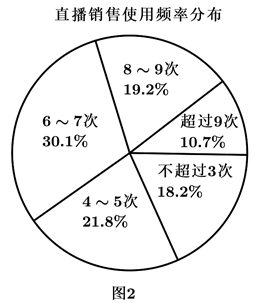
参考数据:独立性检验临界值表
| | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| | 2.072 | 2.706 | 30841 | 5.024 | 6.635 |
其中, .
使用直播销售情况与年龄列联表
| 年轻人 | 非年轻人 | 合计 | |
| 经常使用直播销售用户 | |||
| 不常使用直播销售用户 | |||
| 合计 |
方案一:线下销售.根据市场调研,利用传统的线下销售,到年底可能获利30%,可能亏损15%,也可能不赔不赚,且这三种情况发生的概率分别为 ;
方案二:线上直播销售.根据市场调研,利用线上直播销售,到年底可能获利50%,可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为 .
针对以上两种销售方案,请你从期望和方差的角度为投资公司选择一个合理的方案,并说明理由.
附:
|
|
0.100 |
0.050 |
0.010 |
|
|
2.706 |
3.841 |
6.635 |
|
月份 |
比赛次数 |
主场次数 |
获胜次数 |
主场获胜次数 |
|
10月 |
8 |
3 |
6 |
3 |
|
11月 |
15 |
10 |
8 |
8 |
|
12月 |
14 |
7 |
8 |
5 |
|
1月 |
13 |
4 |
11 |
3 |
|
2月 |
11 |
7 |
6 |
5 |
|
3月 |
14 |
6 |
7 |
3 |
|
4月 |
5 |
3 |
4 |
3 |
(i)若第一场比赛在甲队的主场进行,设整个比赛的进行的局数为 , 求
的分布列及数学期望;
(ii)设选择第一场为甲队的主场的概率为 , 问当
为何值时,无论第一场比赛的场地在哪里,甲队最终获胜的概率相同,并求出此时甲队获胜的概率.
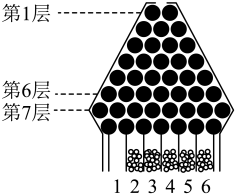
附:若表示投篮的次数,
表示投中的次数,则投中的频率为
;若
, 则
.
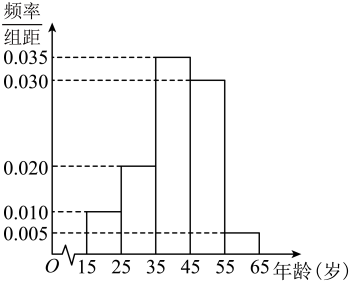
附:若随机变量服从正态分布
, 则:
附表: , 其中
.
a | 0.50 | 0.40 | 0.25 | 0.150 | 0.100 | 0.050 |
0.455 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 |
有兴趣 | 没兴趣 | 合计 | |
男 | |||
女 | |||
合计 |
(i)若比赛最多进行5局,求比赛结束时比赛局数X的分布列及期望E(X)的最大值;
(ii)若比赛不限制局数,写出“甲学员赢得比赛”的概率(用α,β表示),无需写出过程.
门店编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额 | 45 | 33 | 30 | 44 | 28 | 22 | 37 | 21 | 19 | 24 |
门店编号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
销售额 | 34 | 41 | 23 | 20 | 37 | 31 | 29 | 32 | 36 | 42 |

附:若随机变量服从正态分布
, 则
,
,
.
选择餐厅情况(午餐,晚餐) | ||||
王同学 | 9天 | 6天 | 12天 | 3天 |
张老师 | 6天 | 6天 | 6天 | 12天 |
假设王同学、张老师选择餐厅相互独立,用频率估计概率.