2023-2024学年广东省（人教版）九年级（上）数学期末模...

更新时间：2023-12-12 浏览次数：123 类型：期末考试

一、单选题（每题3分，共30分）

1. (2023九上·六安期中) 将一元二次方程 $\text{[math]}$ 化成 $\text{[math]}$ 的形式，则 $\text{[math]}$ （）

A . -1 B . -2023 C . 1 D . 2023

答案解析收藏纠错 + 选题
2. 一块等边三角形木板，边长为1，现将木板沿水平线翻滚(如图)，那么点B从开始至结束所经过的路径长为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 2+ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·丘北月考) 已知关于x的一元二次方程x²-mx+n＝0，其中m，n在数轴上的对应点如图所示，则这个方程的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
4. (2023九上·盐山月考) 已知抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，若关于x的一元二次方程 $\text{[math]}$ （t为实数）在 $\text{[math]}$ 的范围内有解，则t的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·苍溪期末) 如图，点P为⊙O外一点，PA为⊙O的切线，A为切点，PO交⊙O于点B，∠P＝30°，OB＝3，则线段OP的长为（）

A . 3 B . $\text{[math]}$ C . 6 D . 9

答案解析收藏纠错 + 选题
6. (2023九上·深圳月考) 若a、b是关于x的一元二次方程x²－6x＋n＋1＝0的两根，且等腰三角形三边长分别为a、b、4，则n的值为（）

A . 8 B . 7 C . 8或7 D . 9或8

答案解析收藏纠错 + 选题
7. (2021九上·仙居期末) 已知正六边形的边长为4，则这个正六边形外接圆的半径为（）

A . 2 B . 2 $\text{[math]}$ C . 4 D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·香洲期末) 一枚飞任意投掷到如图所示的同心圆镖盘上，此镖盘上有两个同心圆，三条直径把大圆分成六等份，飞镖落在白色区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九上·献县期末) 如图，预防新冠肺炎疫情期间，某校在校门口用塑料膜围成一个临时隔离区，隔离区一面靠长为5m的墙，隔离区分成两个区域，中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m，如果隔离区出入口的大小不计，并且隔离区靠墙的一面不能超过墙长。小明认为：隔离区的最大面积为12m²；小亮认为：隔离区的面积可能为9m²。则：（）

A . 小明正确，小亮错误 B . 小明错误，小亮正确 C . 两人均正确 D . 两人均错误

答案解析收藏纠错 + 选题
10. (2022九上·翁源期末) 如图，抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，经过点 $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④抛物线经过点 $\text{[math]}$ 和 $\text{[math]}$ ，则 $\text{[math]}$ ；⑤ $\text{[math]}$ （ $\text{[math]}$ 为任意实数）．其中，正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·襄城月考) 函数y＝x²﹣5的最小值是．

答案解析收藏纠错 + 选题
12. (2021九上·番禺期末) 抛物线y＝2（x﹣3）²＋7的顶点坐标为．

答案解析收藏纠错 + 选题
13. (2021九上·揭西期末) 若一元二次方程 $\text{[math]}$ 的两根分别为m与n，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2021九上·澄迈期末) 如图，将半径为2，圆心角为90°的扇形BAC绕点A逆时针旋转60°，点B、C的对应点分别为D、E，点D在 $\text{[math]}$ 上，则阴影部分的面积为．

答案解析收藏纠错 + 选题
15. (2022九上·中山期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的内心，则 $\text{[math]}$ 度．

答案解析收藏纠错 + 选题

三、解答题

16. (2018九上·番禺期末) 解答题
1. （1）解方程： $\text{[math]}$ ；
2. （2）用配方法解方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2024九上·南沙期末) 如图，在△ABC中，∠A＝∠B＝30°．
1. （1）尺规作图：在线段AB上找一点O，以O为圆心作圆，使⊙O经过B，C两点．
2. （2）求证：AC与（1）中所做的⊙O相切．
答案解析收藏纠错 + 选题
18. (2021九上·白云期末) 如图， $\text{[math]}$ 是以 $\text{[math]}$ 为斜边的等腰直角三角形，其内部的4段弧均等于以BC为直径的 $\text{[math]}$ 圆周，求图中阴影部分的面积．

答案解析收藏纠错 + 选题
19. (2021九上·香洲期末) 现有A、B两个不透明的袋子，A袋中的两个小球分别标记数字1，2；B袋中的三个小球分别标记数字3，4，5．这五个小球除标记的数字外，其余完全相同．分别将A、B两个袋子中的小球摇匀，然后小明从A、B袋中各随机摸出一个小球，请利用画树状图或列表的方法，求小明摸出的这两个小球标记的数字之和为5的概率．

答案解析收藏纠错 + 选题
20. (2021九上·越秀期末) 某市为鼓励居民节约用水，对居民用水实行阶梯收费，每户居民用水量每月不超过a吨时，每吨按0.3a元缴纳水费；每月超过a吨时，超过部分每吨按0.4a元缴纳水费．
1. （1）若a＝12，某户居民3月份用水量为22吨，则该用户应缴纳水费多少元？
2. （2）若如表是某户居民4月份和5月份的用水量和缴费情况：
  月份
  用水量（吨）
  交水费总金额（元）
  4
  18
  62
  5
  24
  86
  根据上表数据，求规定用水量a的值
答案解析收藏纠错 + 选题
21. (2022·广汉模拟) 如图，已知抛物线y＝﹣x²+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．
1. （1）求抛物线及直线AC的函数关系式；
2. （2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；
3. （3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
22. (2019九上·潮南期末) 为响应荆州市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB＝xm，面积为ym²（如图）．
1. （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
2. （2）若矩形空地的面积为160m² ，求x的值；
3. （3）若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．
  
  甲
  
  乙
  
  丙
  
  单价（元/棵）
  
  14
  
  16
  
  28
  
  合理用地（m²/棵）
  
  0.4
  
  1
  
  0.4
答案解析收藏纠错 + 选题
23. (2022九上·黄埔期末) 如图1， $\text{[math]}$ 为 $\text{[math]}$ 的外接圆，半径为6， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为优弧 $\text{[math]}$ 上异于 $\text{[math]}$ 的一动点，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 平分 $\text{[math]}$ ；
2. （2）如图2， $\text{[math]}$ 平分 $\text{[math]}$ ，且与 $\text{[math]}$ 交于 $\text{[math]}$ ．
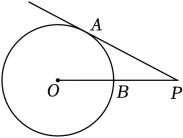
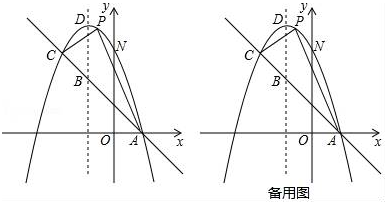
  花花同学认为：无论点 $\text{[math]}$ 运动到哪里，始终有 $\text{[math]}$ ；
  都都同学认为： $\text{[math]}$ 的长会随着点 $\text{[math]}$ 运动而变化．
  你赞同谁的观点，请说明理由；
3. （3）求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题