方法:
;方法
:
;根据以上信息,可以得到的等式是;



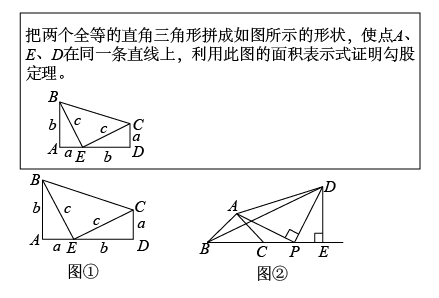
运用“双求法”证明勾股定理勾股定理表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲,它神秘而美妙,证法多样,是数学定理中证明方法最多的定理之一.勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.数学上把这种方法称之为“双求法”. 下面是利用“双求法”证明勾股定理的一种思路: 如图1,将两个全等的直角三角形
|
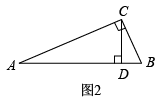
如图2,中,
, CD是AB边上的高,若
,
, 则
.(直接写出答案)


①试探究线段BF,AB,DF之间的数量关系,并说明理由;
②若DF=DC,AD=8,求AB的长度.