备考2024年中考数学核心素养专题二十数与式的存在性问题

更新时间：2024-03-31 浏览次数：52 类型：二轮复习

一、选择题

1. (2024八上·奉化期末) 若关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集中存在负数解，但不存在负整数解，则 $\text{[math]}$ 的取值范围是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·泊头月考) 若a和b都是正整数且 $\text{[math]}$ 和 $\text{[math]}$ 是可以合并的二次根式
结论I：存在两组a和b的值使得 $\text{[math]}$ ；
结论Ⅱ：不存在a和b的值使得 $\text{[math]}$ ．
针对结论I和Ⅱ，下列判断正确的是（）

A . I和Ⅱ都对 B . I和Ⅱ都不对 C . I不对II对 D . I对Ⅱ不对

答案解析收藏纠错 + 选题
3. (2024八上·重庆市期末) 设 $\text{[math]}$ 为正整数，则存在正整数 $\text{[math]}$ 和 $\text{[math]}$ ，使得 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 的值分别为（）.

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九下·义乌月考) 在平面直角坐标系 $\text{[math]}$ 中，对于横、纵坐标相等的点称为“完美点”.下列函数的图象中不存在“完美点”的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·梁平期中) 对多项式 $\text{[math]}$ 任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如： $\text{[math]}$ ， $\text{[math]}$ ， …，给出下列说法：
①至少存在一种“加算操作”，使其结果与原多项式相等；
②不存在任何“加算操作”，使其结果与原多项式之和为0；
③所有的“加算操作”共有8种不同的结果.
以上说法中正确的个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
6. (2023·潼南模拟) 对于五个整式， $\text{[math]}$ ： $\text{[math]}$ ； $\text{[math]}$ ： $\text{[math]}$ ； $\text{[math]}$ ： $\text{[math]}$ ； $\text{[math]}$ ： $\text{[math]}$ ； $\text{[math]}$ ： $\text{[math]}$ 有以下几个结论：
$\text{[math]}$ 若 $\text{[math]}$ 为正整数，则多项式 $\text{[math]}$ 的值一定是正数；
$\text{[math]}$ 存在实数 $\text{[math]}$ ， $\text{[math]}$ ，使得 $\text{[math]}$ 的值为 $\text{[math]}$ ；
$\text{[math]}$ 若关于 $\text{[math]}$ 的多项式 $\text{[math]}$ 为常数 $\text{[math]}$ 不含 $\text{[math]}$ 的一次项，则该多项式 $\text{[math]}$ 的值一定大于 $\text{[math]}$
上述结论中，正确的个数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·金华月考) 已知 $\text{[math]}$ 和 $\text{[math]}$ 均是以 $\text{[math]}$ 为自变量的函数，当 $\text{[math]}$ 时，函数值分别是 $\text{[math]}$ 和 $\text{[math]}$ ，若存在实数 $\text{[math]}$ ，使得 $\text{[math]}$ ，则称函数 $\text{[math]}$ 和 $\text{[math]}$ 具有性质P。以下函数 $\text{[math]}$ 和 $\text{[math]}$ 具有性质P的是（）

A . $\text{[math]}$ 和 $\text{[math]}$ B . $\text{[math]}$ 和 $\text{[math]}$ C . $\text{[math]}$ 和 $\text{[math]}$ D . $\text{[math]}$ 和 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九下·南平模拟) 二次函数 $\text{[math]}$ 的图象上有两个不同的点 $\text{[math]}$ ， $\text{[math]}$ ，给出下列推断：
① 对任意的 $\text{[math]}$ ，都有 $\text{[math]}$ ；② 对任意的 $\text{[math]}$ ，都有 $\text{[math]}$ ；③ 存在 $\text{[math]}$ ， $\text{[math]}$ ，满足 $\text{[math]}$ ，且 $\text{[math]}$ ；④ 对于任意的正实数 $\text{[math]}$ ，存在 $\text{[math]}$ ， $\text{[math]}$ ，满足 $\text{[math]}$ ，且 $\text{[math]}$ .
以上推断中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
9. (2023八上·潼南期中) 在多项式x-y-z-m-n（其中x＞y＞z＞m＞n）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如：x-y-|z-m|-n＝x-y-z+m-n ， |x-y|-z-|m-n|＝x-y-z-m+n ， …．下列说法：
①存在“绝对操作”，使其运算结果与原多项式相等；
②不存在“绝对操作”，使其运算结果与原多项式之和为0；
③所有的“绝对操作”共有7种不同运算结果．
其中正确的个数是（　　）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
10. (2023九上·绍兴月考) 已知 $\text{[math]}$ 和 $\text{[math]}$ 均是以 $\text{[math]}$ 为自变量的函数， $\text{[math]}$ 为实数.当 $\text{[math]}$ 时，函数值分别为 $\text{[math]}$ 和 $\text{[math]}$ ，若存在实数 $\text{[math]}$ ，使得 $\text{[math]}$ .则称 $\text{[math]}$ 和 $\text{[math]}$ 为友好函数，以下 $\text{[math]}$ 和 $\text{[math]}$ 不一定是友好函数的是（）

A . $\text{[math]}$ 和 $\text{[math]}$ B . $\text{[math]}$ 和 $\text{[math]}$ C . $\text{[math]}$ 和 $\text{[math]}$ D . $\text{[math]}$ 和 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024九上·平阴期末) 若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如： $\text{[math]}$ 等都是三倍点”，在 $\text{[math]}$ 的范围内，若二次函数 $\text{[math]}$ 的图象上至少存在一个“三倍点”，则c的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

12. (2024九下·泰州月考) 已知y是关于x的函数，若该函数的图象经过点 $\text{[math]}$ ，则称点P为函数图象上的“平衡点”，例如：直线 $\text{[math]}$ 上存在“平衡点” $\text{[math]}$ ，若函数 $\text{[math]}$ 的图象上存在唯一“平衡点”，则m=．

答案解析收藏纠错 + 选题
13. (2023九上·金堂期中) 若 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ 为常数），则称点 $\text{[math]}$ 为“和谐点”．一次函数 $\text{[math]}$ 存在“和谐点”，则b的取值范围．

答案解析收藏纠错 + 选题
14. (2023八上·石柱月考) 已知关于x的不等式组 $\text{[math]}$ 至少有两个整数解，且存在以3，a，7为边的三角形，则a的整数解有个．

答案解析收藏纠错 + 选题
15. (2023九上·安吉月考) 抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于不同两点 $\text{[math]}$ 、 $\text{[math]}$ ，若存在整数 $\text{[math]}$ 及整数 $\text{[math]}$ ，使得 $\text{[math]}$ 和 $\text{[math]}$ 同时成立，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023九上·忻州期中) 定义：在平面直角坐标系中，对于点 $\text{[math]}$ ，当点 $\text{[math]}$ 满足 $\text{[math]}$ 时，称点 $\text{[math]}$ 是点 $\text{[math]}$ 的“倍增点”．已知点 $\text{[math]}$ ，则正确的结论有．（填写序号）
①点 $\text{[math]}$ 都是点 $\text{[math]}$ 的“倍增点”；
②若直线 $\text{[math]}$ 上的点A是点 $\text{[math]}$ 的“倍增点”，则点A的坐标为 $\text{[math]}$ ；
③抛物线 $\text{[math]}$ 上存在两个点是点 $\text{[math]}$ 的“倍增点”；

答案解析收藏纠错 + 选题
17. (2022九上·东阳月考) 新定义：若一个点的纵坐标是横坐标的2倍，则称这个点为二倍点．若二次函数y＝x²﹣x+c（c为常数）在﹣2＜x＜4的图象上存在两个二倍点，则c的取值范围是．

答案解析收藏纠错 + 选题

三、解答题

18. (2021八下·濉溪期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 是关于x的方程 $\text{[math]}$ 的两个根，是否存在实数m使 $\text{[math]}$ 成立？若存在，求出m的值；若不存在，说明理由.

答案解析收藏纠错 + 选题
19. (2021·汝阳模拟) 已知m，n是方程x²﹣2x﹣1＝0的两个根，是否存在实数a使﹣（m+n）（7m²﹣14m+a）（3n²﹣6n﹣7）的值等于8？若存在，求出a的值；若不存在，请说明理由.

答案解析收藏纠错 + 选题
20. (2020九上·渭滨期中) 已知：关于x的方程 $\text{[math]}$ 是否存在实数m，使方程的两个实数根的平方和等于 $\text{[math]}$ ？若存在，请求出满足条件的m值；若不存在，请说明理由.

答案解析收藏纠错 + 选题
21. (2020九上·垦利期末) 如图，抛物线y＝﹣x²+bx+c与x轴交于A（2，0），B（﹣4，0）两点．
（Ⅰ）求抛物线的解析式；

（Ⅱ）若抛物线交y轴于点C，在抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由；

（Ⅲ）在抛物线第二象限的图象上是否存在一点P，使得△PBC的面积最大？若存在，请直接写出点P的坐标和△PBC面积的最大值；若不存在，请说明理由．

答案解析收藏纠错 + 选题
22. (2023九上·绍兴月考) 若定义：若一个函数图象上存在纵坐标是横坐标2倍的点，则把该函数称为“明德函数”，该点称为“明德点”，例如：“明德函数” $\text{[math]}$ ，其“明德点”为 $\text{[math]}$ .
1. （1） ①判断：函数 $\text{[math]}$ “明德函数”（填“是”或“不是”）；
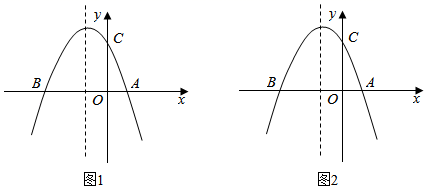
  ②函数 $\text{[math]}$ 的图像上的明德点是；
2. （2）若抛物线 $\text{[math]}$ 上有两个“明德点”，求 $\text{[math]}$ 的取值范围；
3. （3）若函数 $\text{[math]}$ 的图象上存在唯一的一个“明德点”，且当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

四、综合题

23. (2021·秦淮模拟) （概念认识）
已知m是实数，若某个函数图象上存在点M（m，m），则称点M是该函数图象上的“固定点”.

（数学理解）
1. （1）一次函数y＝－2x＋3的图象上的“固定点”的坐标是；
2. （2）求证：反比例函数y＝ $\text{[math]}$ （k＞0）的图象上存在2个“固定点”；
3. （3）将二次函数y＝x²＋bx＋1（b＜－2）的图象在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象在x轴上方的部分组成一个类似“W”形状的新图象.若新图象上恰好存在3个“固定点”，求b的值.
答案解析收藏纠错 + 选题
24. (2023九上·长沙期中) 新定义：已知y是x的函数，若函数图象上存在一点P（a，a+2），则称点P为函数图象上的“朴实点”．例如：直线y＝2x+1上存在的“朴实点”是P（1，3）．
1. （1）判断直线y＝ $\text{[math]}$ x+4上是否有“朴实点”？若有，直接写出其坐标；若没有，请说明理由；
2. （2）若抛物线y＝x²+3x+2-k上存在两个“朴实点”，两个“朴实点”之间的距离为2 $\text{[math]}$ ，求k的值；
3. （3）若二次函数y＝ $\text{[math]}$ x²+（m-t+1）x+2n+2t-2的图象上存在唯一的“朴实点”，且当-2≤m≤3时，n的最小值为t+4，求t的值．
答案解析收藏纠错 + 选题
25. (2021九上·长沙期末) 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于直线x＝n（n为常数）对称，则把该函数称之为“X（n）函数”.
1. （1）在下列关于x的函数中，是“X（n）函数”的，请在相应题目后面的括号中打“√”，不是“X（n）函数”的打“×”.
  ① $\text{[math]}$ （ $\text{[math]}$ ）（   ）
  
  ② $\text{[math]}$ （   ）
  
  ③ $\text{[math]}$ （   ）
2. （2）若关于x的函数 $\text{[math]}$ （h为常数）是“X（2）函数”，与 $\text{[math]}$ （m为常数， $\text{[math]}$ ）相交于A（xA，yA）、B（xB，yB）两点，A在B的左边， $\text{[math]}$ ，求m的值；
3. （3）若关于x的“X（n）函数” $\text{[math]}$ （a，b为常数）经过点（ $\text{[math]}$ ，1），且n＝1，当 $\text{[math]}$ 时，函数的最大值为y₁ ，最小值为y² ，且 $\text{[math]}$ ，求t的值.
答案解析收藏纠错 + 选题
26. (2022九上·普陀月考) 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于y轴对称，则把该函数称之为“T函数”，其图象上关于y轴对称的不同两点叫做一对“T点”．根据该约定，完成下列各题．
1. （1）若点A（1，r）与点B（s，4）是关于x的“T函数”y＝ $\text{[math]}$ 的图象上的一对“T点”，则r＝，s＝，t＝（将正确答案填在相应的横线上）；
2. （2）关于x的函数y＝kx+p（k，p是常数）是“T函数”吗？如果是，指出它有多少对“T点”如果不是，请说明理由；
3. （3）若关于x的“T函数”y＝ $\text{[math]}$ （a＞0，且a，b，c是常数）经过坐标原点O，且与直线l：y＝mx+n（m≠0，n＞0，且m，n是常数）交于M（ $\text{[math]}$ ， $\text{[math]}$ ），N（ $\text{[math]}$ ， $\text{[math]}$ ）两点，当 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ 时，直线l是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由．
答案解析收藏纠错 + 选题
27. (2022九上·长沙期中) 规定：如果两个函数图象上至少存在一对点是关于原点对称的，我们则称这两个函数互为“守望函数”，这对点称为“守望点”．例如：点P（2，4）在函数 $\text{[math]}$ 上，点Q（ $\text{[math]}$ ， $\text{[math]}$ ）在函数 $\text{[math]}$ 上，点P与点Q关于原点对称，此时函数 $\text{[math]}$ 和 $\text{[math]}$ 互为“守望函数”，点P与点Q则为一对“守望点”．
1. （1）函数 $\text{[math]}$ 和函数 $\text{[math]}$ 是否互为“守望函数”？若是，求出它们的“守望点”，若不是，请说明理由；
2. （2）已知函数 $\text{[math]}$ 和 $\text{[math]}$ 互为“守望函数”，求n的最大值并写出取最大值时对应的“守望点”；
3. （3）已知二次函数 $\text{[math]}$ $\text{[math]}$ 与 $\text{[math]}$ 互为“守望函数”，有且仅有一对“守望点”，若二次函数的顶点为M，与x轴交于 $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，又 $\text{[math]}$ ，过顶点M作x轴的平行线l交y轴于点N，直线 $\text{[math]}$ 与y轴交点为点Q，动点E在x轴上运动，求抛物线 $\text{[math]}$ $\text{[math]}$ 上的一点F的坐标，使得四边形 $\text{[math]}$ 为平行四边形．
答案解析收藏纠错 + 选题
28. (2022九下·沭阳模拟) 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于y轴对称，则把该函数称之为“T函数”，其图象上关于y轴对称的不同两点叫做一对“T点”.根据该约定，完成下列各题.
1. （1）若点A（1，r）与点B（s，4）是关于x的“T函数” $\text{[math]}$ 的图象上的一对“T点”，则r＝，s＝，t＝（将正确答案填在相应的横线上）；
2. （2）关于x的函数y＝kx+p（k，p是常数）是“T函数”吗？如果是，指出它有多少对“T点”如果不是，请说明理由；
3. （3）若关于x的“T函数”y＝ax²+bx+c（a＞0，且a，b，c是常数）经过坐标原点O，且与直线l：y＝mx+n（m≠0，n＞0，且m，n是常数）交于M（x₁ ， y₁），N（x₂ ， y₂）两点，当x₁ ， x₂满足（1﹣x₁）﹣¹+x₂＝1时，直线l是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由.
答案解析收藏纠错 + 选题

五、实践探究题

29. (2020九下·宁晋开学考) 发现：五个连续的偶数中，存在前三个偶数的平方和等于后两个偶数的平方和．
验证：
1. （1） $\text{[math]}$
2. （2）若还存在五个连续的偶数，前三个偶数的平方和可以等于后两个偶数的平方和，设中间的偶数为n，求n
3. （3）延伸：是否存在三个连续的奇数中，有前两个奇数的平方和可以等于后一个奇数的平方，请说明理由．
答案解析收藏纠错 + 选题
30. (2023九上·雨花月考) 【创新是民族进步的灵魂 $\text{[math]}$ 华为一直在科技领域追求极致美学、极致工艺、极致创新 $\text{[math]}$ 真正意义上做到遥遥领先 $\text{[math]}$ 】我们不妨约定：若 $\text{[math]}$ ， $\text{[math]}$ 是关于 $\text{[math]}$ 的函数，当 $\text{[math]}$ 时，总有 $\text{[math]}$ ，并存在 $\text{[math]}$ 满足 $\text{[math]}$ ，使得 $\text{[math]}$ ，我们则称函数 $\text{[math]}$ 对 $\text{[math]}$ 在 $\text{[math]}$ 领域“ $\text{[math]}$ 阶领先”．
1. （1）已知一次函数 $\text{[math]}$ 对 $\text{[math]}$ 在 $\text{[math]}$ 领域“ $\text{[math]}$ 阶领先”，求 $\text{[math]}$ 的值；
2. （2）已知二次函数 $\text{[math]}$ 为常数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，其横坐标分别记为 $\text{[math]}$ 和 $\text{[math]}$ ，且满足 $\text{[math]}$ ，请判断二次函数 $\text{[math]}$ 对一次函数 $\text{[math]}$ 能否在 $\text{[math]}$ 领域“ $\text{[math]}$ 阶领先”，请说明理由；
3. （3）已知二次函数 $\text{[math]}$ 的顶点经过一次函数 $\text{[math]}$ 的图象，若二次函数 $\text{[math]}$ 对一次函数 $\text{[math]}$ 在 $\text{[math]}$ 领域“ $\text{[math]}$ 阶领先”，求二次函数 $\text{[math]}$ 的解析式．
答案解析收藏纠错 + 选题