
 B .
B .  C .
C .  D .
D . 
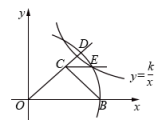
①双曲线的解析式为;②
点的坐标是
;③
;④
. 其中正确的结论有( )
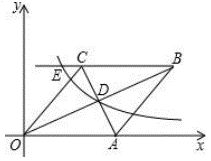
①若点到
轴的距离小于4,求
的取值范围;
②当时,若
, 求
的值.
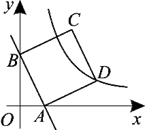
设矩形相邻两边的长分别为 , 由矩形的面积为4,得
, 即
;由周长为
, 得
, 即
. 满足要求的
应是两个函数图象在第象限内的交点的坐标.
函数的图像如图所示,而函数
的图像可由直线
平移得到.请在同一直角坐标系中直接画出直线
.
当直线平移到与函数的图像有唯一交点
时,写出周长
的值;
若能生产出面积为4的矩形模具,求出周长的取值范围.(直接写出结论)
小丽学习了方程、不等式、函数后提出如下问题:如何求不等式 方法1方程 |
任务: