2024年人教版中考数学二轮复习专题20 数据分析

更新时间：2024-04-16 浏览次数：10 类型：二轮复习

一、单选题

1. 在一次定点投篮训练中，五位同学投中的个数分别为3，4，4，6，8，则关于这组数据的说法不正确的是（　　）

A . 平均数是5 B . 中位数是6 C . 众数是4 D . 方差是3.2

答案解析收藏纠错 + 选题
2. (2024·五华模拟) 2024年1月24日上午云南省第十四届人民代表大会第二次会议开幕，省长王予波代表省人民政府向大会作政府工作报告．报告指出，2023年是全面贯彻党的二十大褚神的开局之年，是三年新冠疫情防控转移后经济恢复发展的一年，也是本届政府依法履职的第一年．这一年，云南省经济总量首次突破3万亿元大关，新时代以来，我省经济总量继2012年迈上1万亿元台阶后，用6年时间、在2018年迈上2万亿元台阶，面对世纪疫情等超预期因素的影响，用5年时间、在2023年首次突破3万亿元大关，站在了新的发展起点上。下面是云南省2018年至2023年经济总量的条形统计图
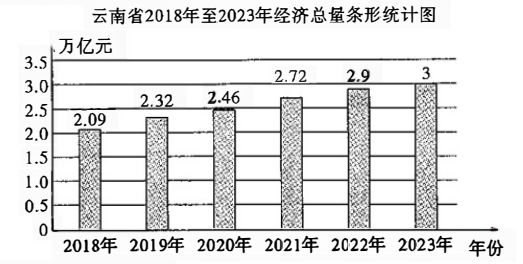
根据统计图得出如下结论，其中正确的是（）

A . 这6年中，云南省经济总量年增长率均逐年增加 B . 这6年中，2023年云南省的经济总量比2018年翻一番 C . 这6年中，云南省经济总量均逐年增加 D . 这6年中，云南省经济总量的平均值超过2.72万亿元

答案解析收藏纠错 + 选题
3. (2022·恩施) 为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如下表所示：
月用水量（吨）
3
4
5
6
户数
4
6
8
2
关于这若干户家庭的该月用水量的数据统计分析，下列说法正确的是（）

A . 众数是5 B . 平均数是7 C . 中位数是5 D . 方差是1

答案解析收藏纠错 + 选题
4. (2021八下·梁园期末) 小丽在本学期的数学成绩分别为：平时测验成绩为93分，期中考试成为90分，期末考试成绩为95分，按照平时、期中、期末所占比例为10%，30%，60%计算小丽本学期的总评成绩应该是（）

A . 92.5分 B . 92.8分 C . 93.1分 D . 93.3分

答案解析收藏纠错 + 选题
5. (2022八下·嵊州期末) 已知5个正数a，b，c，d，e 的平均数是m，且 $\text{[math]}$ ，则数据 a，b，c，0，d，e的平均数和中位数是（）

A . m， $\text{[math]}$ B . m， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·桥东模拟) 刘老师从某校2000名学生每天体育锻炼时长的问卷中，随机抽取部分学生的答卷，将这部分学生的锻炼时长作为一个样本进行研究，并将结果绘制成如图的条形统计图，其中一部分被墨迹遮盖，已知每天锻炼时长为1小时的学生人数占样本总人数的36%，则下列说法正确的是（）

A . 样本容量小于200 B . 2000名学生是总体 C . 锻炼时长为1.5小时是这个样本的众数 D . 该校锻炼用时为2小时的学生约有200名

答案解析收藏纠错 + 选题
7. (2021·埇桥模拟) 某企业2020年6～10月生产利润的变化情况如折线图所示，下列说法与图中反映的信息相符的是（）．

A . 6～7月份利润的增长快于7～8月份利润的增长 B . 6～10月份利润的方差为14000（万元）² C . 6～10月份利润的众数是1300万元 D . 6～10月份利润的中位数为1300万元

答案解析收藏纠错 + 选题
8. (2022八下·新兴期末) 某校八年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（）

A . 平均数 B . 众数 C . 中位数 D . 都可以

答案解析收藏纠错 + 选题
9. (2021九上·贵阳期末) 小明将贵州健康码打印在面积为 $\text{[math]}$ 的正方形纸上，如图所示为了估计图中健康码部分的面积，在纸内随机掷点，经过大量重复试验，发现点落入健康码部分的频率稳定在0.6左右，据此可以估计健康码部分的面积约为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·北部湾月考) 下列说法中，正确的是（）

A . 一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中位数是 $\text{[math]}$
B . 质检部门要了解一批灯泡的使用寿命，应当采用普查的调查方式
C . 购买一张福利彩票中奖是一个确定事件
D . 分别写有三个数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的三张卡片 $\text{[math]}$ 卡片的大小形状都相同 $\text{[math]}$ ，从中任意抽取两张，则卡片上的两数之积为正数的概率为 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023·增城模拟) 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差：

	甲	乙	丙
平均数	9.23	9.3	9.3
方差	0.23	0.017	0.057

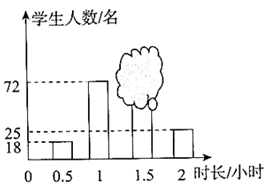
根据表中的数据，要选择一名成绩好且发挥稳定的学生参加比赛，应选择．

答案解析收藏纠错 + 选题

12. (2023·长沙模拟) 春日好时光，读书正当时，在第 $\text{[math]}$ 个世界读书日来临之际， $\text{[math]}$ 月 $\text{[math]}$ 日，由省教育厅等八个部门联合主办的 $\text{[math]}$ 年河南省青少年学生读书行动启动仪式暨河南省中小学书香校园建设现场会在漯河市举行．河南某中学以此次活动为契机，举行相关朗诵比赛，更好的落实五育并举的教育方针，促进师生珍惜时光、广泛阅读、下面是甲、乙、丙三名参赛选手的成绩如表所示，每名选手的成绩由观众评分和评委评分两部分组成：

评分人	评分权重	甲	乙	丙
观众（学生）	$\text{[math]}$	$\text{[math]}$ 分	$\text{[math]}$ 分	$\text{[math]}$ 分
评委（老师）	$\text{[math]}$	$\text{[math]}$ 分	$\text{[math]}$ 分	$\text{[math]}$ 分

经过最后汇总，总分最高的是选手（填“甲、乙、丙”）．

答案解析收藏纠错 + 选题

13. (2021七下·西城期中) 在1～7月份，某种水果的每斤进价与每斤售价的信息如图所示，则出售该种水果每斤利润最大的月份是月份．

答案解析收藏纠错 + 选题
14. (2022八下·龙港期中) 某厂家2021年1～5月份的口罩产量统计图如图所示，3月份口罩产量不小心被墨汁覆盖，已知2月份到4月份该厂家每个月口罩产量的月增长率都相同，则3月份口罩产量为万只.

答案解析收藏纠错 + 选题

15. (2022·山西) 生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多，为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位： $\text{[math]}$ ），结果统计如下：

品种	第一株	第二株	第三株	第四株	第五株	平均数
甲	32	30	25	18	20	25
乙	28	25	26	24	22	25

则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）．

答案解析收藏纠错 + 选题

16. (2023·怀化模拟) 近年来，洞庭湖区环境保护效果显著，南迁的候鸟种群越来越多 $\text{[math]}$ 为了解南迁到该区域某湿地的 $\text{[math]}$ 种候鸟的情况，从中捕捉 $\text{[math]}$ 只，戴上识别卡并放回；经过一段时间后观察发现， $\text{[math]}$ 只 $\text{[math]}$ 种候鸟中有 $\text{[math]}$ 只佩有识别卡，由此估计该湿地约有只 $\text{[math]}$ 种候鸟．

答案解析收藏纠错 + 选题
17. (2023·茶陵模拟) 统计某天 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ 经过某高速公路某测速点的汽车速度，得到如右所示的频数分布直方图 $\text{[math]}$ 每一组不含前一个边界值，含后一个边界值 $\text{[math]}$ 若该路段汽车限速为 $\text{[math]}$ 含 $\text{[math]}$ ，则超速行驶的汽车占全部汽车的 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

18. (2023八上·深圳期中) 八年级二班举办了主题为“致敬航天人，共筑星河梦”的演讲比赛．由学生1，学生2，老师、班长一起组成四人评委团，对演讲者现场打分，满分10分．图1是甲、乙二人的演讲得分的不完整折线图，已知二人得分的平均数都是8分．
1. （1）班长给乙的打分是 ▲ 分，补全折线图；
2. （2）在参加演讲的同学中，如果某同学得分的四个数据的方差越小，则认为评委对该同学演讲的评价越一致．请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致；
3. （3）要在甲、乙两位同学中选出一人参加年级的演讲比赛．按照扇形统计图（图2）中各评委的评分占比，分别计算两人各自的最后得分，得分高的能被选中，请判断谁被选中．
答案解析收藏纠错 + 选题
19. (2024八上·龙岗期末) 为了解学生的体育锻炼情况，学校以“活跃校园---探索初中生的运动生活”为主题开展调查研．通过问卷，收集了八、九年级学生的平均每周锻炼时长数据，现从两个年级分别随机抽取10名学生的平均每周锻炼时长（单位：小时）进行统计：
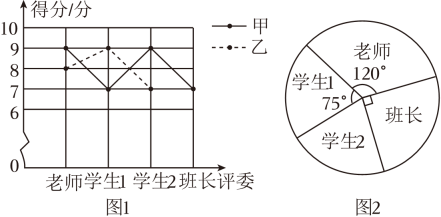
八年级9，8，11，8，7，5，6，8，6，12
九年级9，7，6，9，9，10，8，9，7，6
整理如下：
年级
平均数
中位数
众数
方差
八年级
8
a
8
4.89
九年级
8
8.5
b
2
根据以上信息，回答下列问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2） A同学说：“我平均每周锻炼 $\text{[math]}$ 小时，位于年级中等偏上水平”，由此可判断他是年级的学生；
3. （3）你认为哪个年级的学生体育锻炼情况的总体水平较好？请给出一条理由．
答案解析收藏纠错 + 选题
20. (2023七下·庐江期末) 《如果想毁掉一个孩子，就给他一部手机！》这是微信圈一篇热传的文章．国际上，法国教育部宣布从 $\text{[math]}$ 年 $\text{[math]}$ 月新学期起小学和初中禁止学生使用手机．为了解学生手机使用情况，学校随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，已知“查资料”的人数是 $\text{[math]}$ 人．请你根据以上信息解答下列问题：

（ $\text{[math]}$ 表示大于 $\text{[math]}$ 同时小于或等于 $\text{[math]}$ ，以下类推）
1. （1）补全条形统计图；
2. （2）在扇形统计图中，“玩游戏”对应的圆心角度数是度；
3. （3）某校共有学生 $\text{[math]}$ 人，估计每周使用手机时间在 $\text{[math]}$ 小时以上（不含 $\text{[math]}$ 小时）的人数．
答案解析收藏纠错 + 选题

21. (2023八下·泗水期末) 某校开展“远离溺水·珍爱生命”安全知识竞赛，现从该校七、八年级中各随机抽取15名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示），共分为五个等级：A ． $\text{[math]}$ ， B ． $\text{[math]}$ ， C ． $\text{[math]}$ ， D ． $\text{[math]}$ ， E ． $\text{[math]}$ ，

下面给出了部分信息：

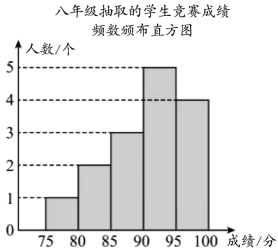
七年级15个学生的竞赛成绩：78，83，89，97，98，85，100，94，87，90，93，92，99，95，100

八年级15个学生的竞赛成绩中D等级包含的所有数据为：91，92，94，90，93

七、八年级中各随机抽取15名学生的竞赛成绩统计表

年级	平均数	众数	中位数	方差
七年级	92	a	93	41.7
八年级	92	87	b	50.2

（1）根据以上信息，可以求出； $\text{[math]}$ ， $\text{[math]}$ ；
（2）根据以上数据，你认为哪个年级的学生的竞赛成绩较好，请从两个不同的角度说明理由．
（3）若规定评分90分及以上为优秀，若参加知识竞赛的七年级有1200人，八年级有1500人，请估算两个年级学生评分为优秀的学生共有多少人．

答案解析收藏纠错 + 选题

四、综合题

22. (2021九下·福州开学考) 今年2-4月某市出现了200名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗.图1是该市轻症、重症、危重症三类患者的人数扇形统计图（不完整），图2是这三类患者的人均治疗费用统计图，请回答下列问题：
1. （1）轻症患者的人数是多少？
2. （2）所有患者的平均治疗费用是多少万元？
3. （3）由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的A、B、C、D、E五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中B、D两位患者的概率.
答案解析收藏纠错 + 选题
23. (2023·交城模拟) 2022年4月21日新版义务教育课程方案及各科课程标准正式颁布，新的课程标准优化了课程设置，其中将劳动教育从综合实践活动课程中独立出来．某校为了初步了解学生的劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查．下图是根据此次调查得到的结果绘制的两幅不完整统计图表．
学生平均每周劳动时间的统计表
组别
时间（小时）
频数（人）
A
$\text{[math]}$
130
B
$\text{[math]}$
180
C
$\text{[math]}$
85
D
$\text{[math]}$
85
E
$\text{[math]}$
$\text{[math]}$
学生最喜欢的劳动课程统计图
请根据统计图表回答下列问题：
1. （1）本次调查中，平均每周劳动时间不少于3小时的人数占被调查人数的百分比为；
2. （2）若该校有2000名学生，请估计最喜欢的劳动课程为种植的有多少人？
3. （3）请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．
答案解析收藏纠错 + 选题
24. (2022·珠海模拟) 从2021年秋季开学以来，全国各地中小学都开始实行了“双减政策”．为了解家长们对“双减政策”的了解情况，从某校1200名家长中随机抽取部分家长进行问卷调查，调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．
1. （1）本次抽取家长共有人，扇形图中“基本了解”所占扇形的圆心角是；
2. （2）估计此校“非常了解”和“了解较多”的家长共有多少人?
3. （3）学校计划从“了解较少”的家长中抽取1位初一学生家长，1位初二学生家长，2位初三学生家长参加培训，若从这4位家长中随机选取两人作为代表，请通过列表或面树状图的方法求所选出的两位家长既有初一家长，又有初二家长的概率．
答案解析收藏纠错 + 选题

25. (2023七下·北京市期末) 华罗庚先生是中国著名数学家．为激励中国数学家在发展中国数学事业中做出突出贡献设立了“华罗庚数学奖”．小聪对截止到2023年第十六届“华罗庚数学奖”得主获奖时的年龄（单位：岁）进行收集、整理，绘制成如下的频数分布表，频数分布直方图和扇形统计图．

年龄分组	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	3	1	11	7	$\text{[math]}$	3	2

根据以上信息，回答下列问题

（1）写出 $\text{[math]}$ 的值是，截止到第十六届共有人获得“华罗庚数学奖”；
（2）补全“华罗庚数学奖”得主获奖年龄频数分布直方图；
（3）第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为68岁，他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄（填“小”或“大”），理由是．

答案解析收藏纠错 + 选题

五、实践探究题

26. (2022九上·潞城月考) 综合与实践
1. （1）【问题再现】
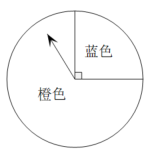
  课本中有这样一道概率题：如图1，这是一个可以自由转动的转盘，转动转盘，当转盘停止时，指针落在蓝色区域和橙色区域的概率分别是多少？请你解答．
2. （2）【类比设计】
  在元旦晚会上班长想设计一个摇奖转盘．请你在图2中设计一个转盘，自由转动这个转盘，当它停止转动时，三等奖：指针落在红色区域的概率为 $\text{[math]}$ ，二等奖：指针落在白色区域的概率为 $\text{[math]}$ ，一等奖：指针落在黄色区域的概率为 $\text{[math]}$ ．
3. （3）【拓展运用】
  在一次促销活动中，某商场为了吸引顾客，设立转盘，转盘被平均分为10份，顾客每消费200元转动1次，对准红1份，黄2份、绿3份区域，分别得奖金100元、50元、30元购物券，求转动1次所获购物券的平均数．
答案解析收藏纠错 + 选题

27. (2023八下·盘龙期末) 【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．

【实践发现】同学们随机收集芒果树、荔枝树的树叶各 $\text{[math]}$ 片，通过测量得到这些树叶的长 $\text{[math]}$ 单位： $\text{[math]}$ ，宽 $\text{[math]}$ 单位： $\text{[math]}$ 的数据后，分别计算长宽比，整理数据如下：

	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
芒果树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
荔枝树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
荔枝树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

【问题解决】

（1） a= ， $\text{[math]}$ ， $\text{[math]}$ ；
（2） A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大 $\text{[math]}$ ”
$\text{[math]}$ 同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍 $\text{[math]}$ ”以上两位同学的说法中，合理的是同学；
（3）现有一片长 $\text{[math]}$ ，宽 $\text{[math]}$ 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．