 B .
B . 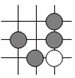 C .
C . 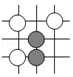 D .
D . 
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
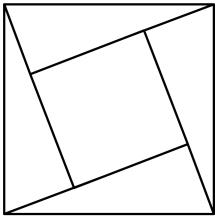


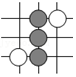
请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠;(2)所设计的图案(不含方格纸)必须一个是中心对称图形,另一个是轴对称图形.

阅读下列材料并完成相应的任务.
|
我国是最早了解和应用勾股定理的国家之一,古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用,古希腊数学家毕达哥拉斯首先证明了勾股定理,在西方,勾股定理又称为“毕达哥拉斯定理”.关于勾股定理的研究还有一个很重要的内容是勾股数组,在课本中我们已经了解到“能够成为直角三角形三条边的三个正整数称为勾股数”. 以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法: 方法1:若m为奇数 方法2:若任取两个正整数m和 |
任务:


|
运往地 |
|
|
|
|
运费(元/袋) |
20 |
10 |
15 |