命题新趋势2 学科融合——2024年浙教版数学七（下）期末复...

更新时间：2024-06-04 浏览次数：40 类型：复习试卷

一、选择题

1. (2024·大余模拟) 物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变．如图，我们建立折射现象数学模型， $\text{[math]}$ 表示水面，它与底面 $\text{[math]}$ 平行，光线 $\text{[math]}$ 从空气射入水里时发生了折射，变成光线 $\text{[math]}$ 射到水底 $\text{[math]}$ 处，射线 $\text{[math]}$ 是光线 $\text{[math]}$ 的延长线．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022七下·蜀山期末) 据中新网报道，中国科学技术大学完成的“祖冲之二号”和“九章二号”量子计算优越性实验入选2021年国际物理学十大进展，人们发现全球目前最快的超级计算机用时2.3秒的计算量，“祖冲之二号”大约用时仅为0.00000022秒，将数字0.00000022用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·高碑店期末) 氧气是由氧元素形成的一种单质，氧元素的原子半径约为 $\text{[math]}$ ，则氧原子的半径用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·贺州月考) 生物具有遗传多样性，遗传信息大多储存在 $\text{[math]}$ 分子上，一个 $\text{[math]}$ 分子的直径约为 $\text{[math]}$ ． $\text{[math]}$ 用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·合肥期末) 世界最小生物，是澳大利亚昆士兰大学的科学家在外海由钻油平台从海底下约 $\text{[math]}$ 公里深处挖出的沙岩中发现的生物，它们的身长只有 $\text{[math]}$ 米，小于细胞，甚至比已知的最小细菌还要小，体积大概和病毒差不多．因此，这种生物刷新了地球生物最小体积的记录，其中 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022七下·盂县期中) 在我们常见的英文字母中，也存在着同位角、内错角，在下面几个字母中，含有内错角最少的字母是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023七下·金牛期中) 反物质理论是当代物理研究中的重大突破，科学家们一直在致力于寻找反物质存在的证据，现捕捉到某种微粒子，测得它的质量为0.0000000674克，这个质量用科学记数法表示为（）

A . $\text{[math]}$ 克 B . $\text{[math]}$ 克 C . $\text{[math]}$ 克 D . $\text{[math]}$ 克

答案解析收藏纠错 + 选题
8. (2023七下·北仑期中) 如图1，当光线从空气进入水中时，会发生折射，满足入射角∠1与折射角∠2的度数比为5：4．如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水面夹角分别为α，β，在水中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ γ D . α+β＝180°﹣γ

答案解析收藏纠错 + 选题
9. (2024七下·高州月考) 某种生物孢子的直径为0.000063m，这个数据用科学记数法表示为（）

A . 0.63×10^－⁵ B . 0.63×10^－⁶ C . 6.3×10^－⁵ D . 6.3×10^－⁶

答案解析收藏纠错 + 选题
10. (2024七下·寿阳期中) 随着人类基因组（测序）计划的逐步实施以及分子生物学相关学科的迅猛发展，越来越多的动植物、微生物基因组序列得以测定，已知某种基因芯片每个探针单元的面积为 $\text{[math]}$ ，将 $\text{[math]}$ 用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023七下·红桥期末) 地理老师介绍到：长江比黄河长836千米，黄河长度的6倍比长江长度的5倍多1284千米，小东根据地理教师的介绍，设长江长为 $\text{[math]}$ 千米，黄河长为 $\text{[math]}$ 千米，然后通过列、解二元一次方程组，正确的求出了长江和黄河的长度，那么小东列的方程组可能是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

12. 埃是表示极小长度的单位名称，是为纪念瑞典物理学家埃斯特朗而命名的.1埃等于一亿分之一厘米，用科学记数法表示：1埃等于cm．

答案解析收藏纠错 + 选题
13. (2023七下·凤凰期末) 物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变．如图，我们建立折射现象数学模型， $\text{[math]}$ 表示水面，它与底面 $\text{[math]}$ 平行，光线 $\text{[math]}$ 从空气射入水里时发生了折射，变成光线 $\text{[math]}$ 射到水底 $\text{[math]}$ 处，射线 $\text{[math]}$ 是光线 $\text{[math]}$ 的延长线， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为°．

答案解析收藏纠错 + 选题
14. (2024·瑞昌模拟) 如图，平行于主光轴 $\text{[math]}$ 的光线 $\text{[math]}$ 和 $\text{[math]}$ 经过凹透镜的折射后，折射光线 $\text{[math]}$ 的反向延长线交于主光轴 $\text{[math]}$ 上一点P ． $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
15. 从汽车灯的点 $\text{[math]}$ 处发出的一束光线经灯的反光罩反射后沿 $\text{[math]}$ 方向平行射出，已知入射光线 $\text{[math]}$ 的反射光线为 $\text{[math]}$ ．在如图所示的截面内，若入射光线 $\text{[math]}$ 经反光罩反射后沿 $\text{[math]}$ 射出，且 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2024七下·渭城期中) 某种樱桃营养丰富，富含铁、维生素A、B、C及钙、磷等矿质元素．每克该种樱桃含维生素C不低于 $\text{[math]}$ 克．将 $\text{[math]}$ 用科学记数法表示为．

答案解析收藏纠错 + 选题
17. (2022八下·洪江期末) “新冠肺炎”翻译成英文为“novelcoronavirus”那么英文单词“novelcoronavirus”中“O”出现的频率是.

答案解析收藏纠错 + 选题
18. (2022七下·淮安月考) DNA是每一个生物携带自身基因的载体，它是遗传物质脱氧核糖核酸的英文简称，DNA分子的直径只有0.000000736cm，则这个数用科学记数法表示是.

答案解析收藏纠错 + 选题
19. (2024七下·临泽期中) 碳纳米管的硬度与金刚石相当，却拥有良好的柔软性，我国某物理研究组已研制出直径为0.00000000052米的碳纳米管，将0.00000000052用科学记数法表示为．

答案解析收藏纠错 + 选题
20. (2023七下·顺德期中) 如图是某灯具的镜面反射示意图，从光源点 $\text{[math]}$ 处发出的光线 $\text{[math]}$ ， $\text{[math]}$ 经弯曲的镜面反射后射出，且满足反射光线 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
21. (2024八下·晋江期中) 每个生物携带自身基因的载体是生物细胞的 $\text{[math]}$ ． $\text{[math]}$ 分子的直径只有 $\text{[math]}$ ，它们在细胞核的染色体上，按一定顺序排列成螺旋形的独特结构．将0.0000002用科学记数法表示是．

答案解析收藏纠错 + 选题

三、解答题

22. 在弹性限度内，弹簧总长 y(cm)与所挂物体质量 x(kg)满足公式：y=kx+b(k，b为常数且k ≠0).当挂 1 kg 物体时，弹簧总长为6.3cm；当挂4k g物体时，弹簧总长为7.2cm，则公式中b的值为

答案解析收藏纠错 + 选题
23. 把太阳看作一个球体，用V，r分别表示太阳的体积和半径，有公式V= $\text{[math]}$ πr³ ．已知太阳的半径约为6×10⁵km，则太阳的体积大约是多少立方千米(π取3) ？

答案解析收藏纠错 + 选题
24. (2024七下·金沙月考) 如图，在台球运动中（每次撞击桌边时，撞击前后的路线与桌边所成的夹角相等），如果母球P击中桌边点A ，经桌边反弹后击中相邻的另一桌边点B ，然后又反弹击中球C ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
2. （2）母球P经过的路线 $\text{[math]}$ 与 $\text{[math]}$ 一定平行吗？请说明理由．
答案解析收藏纠错 + 选题
25. 太阳系4个内行星的直径，以及与太阳的平均距离如下：
地球：直径是12756 km，与太阳的平均距离是 $\text{[math]}$
金星：直径是12104 km，与太阳的平均距离是 $\text{[math]}$
火星：直径是6794km，与太阳的平均距离是 $\text{[math]}$
水星：直径是4878km，与太阳的平均距离是 $\text{[math]}$
为了解这4个内行星的大小和距离太阳的远近情况，你将怎样重新整理这些数据? 将它们按照你的方法进行整理.

答案解析收藏纠错 + 选题
26. (2023七下·灵丘期中) 阅读下列材料，完成相应任务．
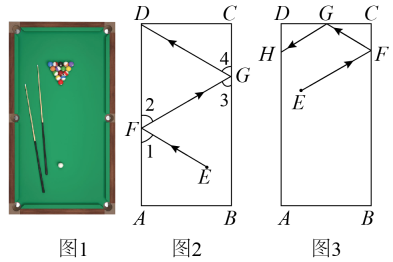
台球中的数学
如图1是台球桌面实物图，图2是抽象出的数学图形，已知长方形桌面 $\text{[math]}$ 中， $\text{[math]}$ ，一个球在桌面上的点 $\text{[math]}$ 处滚向桌边 $\text{[math]}$ ，碰到 $\text{[math]}$ 上的点 $\text{[math]}$ 后反弹，再碰到 $\text{[math]}$ 边上的点 $\text{[math]}$ 后，再次反弹进入底袋点 $\text{[math]}$ ．在球碰到桌边反弹的过程中，击出线与桌边的夹角 $\text{[math]}$ 等于反弹线与桌边的夹角 $\text{[math]}$ ，同理 $\text{[math]}$ ．
1. （1）任务一：如图2，求证： $\text{[math]}$ ；
2. （2）任务二：如图3，若球在桌面的点 $\text{[math]}$ 处，经过两次反弹后碰到 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，若 $\text{[math]}$ ，请你判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由．
答案解析收藏纠错 + 选题

四、作图题

27. (2023·百色模拟) 如图，在平面直角坐标系中，形如英文字母“V”的图形三个端点的坐标分别是A(2，3)，B(1，0)，C(0，3).
1. （1）画出“V”字图形向左平移2个单位后的图形；
2. （2）画出原“V”字图形关于x轴对称的图形；
3. （3）所得图形与原图形结合起来，你能从中看出什么英文字母？（任意答一个即可）
答案解析收藏纠错 + 选题

五、实践探究题

28. (2024七下·金州月考) 在物理学中，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．
如图1，一束光线 $\text{[math]}$ 射到平面镜 $\text{[math]}$ 上，被 $\text{[math]}$ 反射后的光线为 $\text{[math]}$ ，则入射光线 $\text{[math]}$ 、反射光线 $\text{[math]}$ 与平面镜 $\text{[math]}$ 所夹的锐角 $\text{[math]}$ ．
1. （1）【简单应用】
  如图2，有一口井，已知入射光线 $\text{[math]}$ 与水平线 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，现放置平面镜 $\text{[math]}$ ，可使反射光线 $\text{[math]}$ 正好垂直照射到井底（即射线 $\text{[math]}$ ）， $\text{[math]}$ 与水平线的夹角 $\text{[math]}$ 的度数为．
2. （2）【类比拓展】
  如图3，有两块平面镜 $\text{[math]}$ ，且 $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过两次反射，得到反射光线 $\text{[math]}$ ．由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即： $\text{[math]}$ ．在这样的条件下，求证： $\text{[math]}$ ．
3. （3）【尝试探究】
  两块平面镜 $\text{[math]}$ ，且 $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过两次反射，得到反射光线 $\text{[math]}$ ．如图4，光线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是多少？（用含 $\text{[math]}$ 的式子表示）（三角形内角和 $\text{[math]}$ ）
答案解析收藏纠错 + 选题
29. (2024七下·威县月考) 【阅读】如图1，光线从空气中射入玻璃砖时，光线的传播方向发生了改变，即玻璃砖中的光线与原来空气中的光线不在同一条直线上，这是光线在玻璃砖中的折射现象．
【探究】为了探究光折射时的特点，科学实验小组将一束光 $\text{[math]}$ 斜射到一块玻璃砖的上表面 $\text{[math]}$ 上的点 $\text{[math]}$ 处，并在下表面 $\text{[math]}$ （ $\text{[math]}$ ）的点 $\text{[math]}$ 处射出， $\text{[math]}$ 于点 $\text{[math]}$ ，如图2所示，图中所有的点都在同一平面内，查问相关科学知识，得到 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求光的传播方向改变了多少度；
2. （2）请判断射入光线 $\text{[math]}$ 与射出光线 $\text{[math]}$ 是否平行，并说明理由；
3. （3）已知光线 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为35°，如图3所示．若射出光线 $\text{[math]}$ 与光线 $\text{[math]}$ 垂直，则 $\text{[math]}$ 的度数为．
答案解析收藏纠错 + 选题
30. (2024七下·平山月考) 【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角r等于入射角i ．这就是光的反射定律．
1. （1）学完光的反射定律，数学兴趣小组的同学想利用这个定律结合数学知识制作一个简易潜望镜，并画出了潜望镜的工作原理示意图，如图2所示，AB、CD是平行放置的两面平面镜，已知光线经过平面镜反射时、有∠2＝∠1，∠4＝∠3，请问进入潜望镜的光线EF和离开潜望镜的光线GH是否平行，说明理由．
2. （2） 【尝试探究】
  把两个平面镜AB ， BC按图3所示位置放置， $\text{[math]}$ ，光线经过两次反射后，∠2＝∠1，∠4＝∠3，反射光线GH与入射光线EF平行但方向相反、求 $\text{[math]}$ 的度数．【注：三角形的三个角的和是180°】
答案解析收藏纠错 + 选题
31. (2023七下·深圳期中) 如图
【学习新知】：
射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1， $\text{[math]}$ 是平面镜，若入射光线与水平镜面夹角为 $\text{[math]}$ ，反射光线与水平镜面夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．
1. （1）【初步应用】：
  生活中我们可以运用“激光”和两块相交的平面镜进行测距．如图2当一束“激光” $\text{[math]}$ 射入到平面镜 $\text{[math]}$ 上、被平面镜 $\text{[math]}$ 反射到平面镜 $\text{[math]}$ 上，又被平面镜 $\text{[math]}$ 反射后得到反射光线 $\text{[math]}$ ．回答下列问题：
  ①当 $\text{[math]}$ ， $\text{[math]}$ （即 $\text{[math]}$ ）时，求 $\text{[math]}$ 的度数．
  ②当 $\text{[math]}$ 时，任何射入平面镜 $\text{[math]}$ 上的光线 $\text{[math]}$ 经过平面镜 $\text{[math]}$ 和 $\text{[math]}$ 的两次反射后，入射光线 $\text{[math]}$ 与反射光线 $\text{[math]}$ 总是平行的．请你根据所学过的知识及新知说明．
  （提示：三角形的内角和等于 $\text{[math]}$ ）
2. （2）【拓展探究】：
  如图3，有三块平面镜 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过三次反射，得到反射光线 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，若要使 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题

六、综合题

32. (2023七下·哈尔滨期末) 虹桥中学计划为地理兴趣小组购买大、小两种地球仪，若购买1个大地球仪和3个小地球仪需要136元；若购买2个大地球仪和1个小地球仪需要132元．
1. （1）求每个大地球仪和每个小地球仪各多少元；
2. （2）学校决定购买以上两种地球仪共30个，总费用不超过1080元，那么虹桥中学最多可以购买多少个大地球仪？
答案解析收藏纠错 + 选题
33. (2023七下·瓯海期中) 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.
1. （1）提词器的原理如图①，AB表示平面镜，CP表示入射光线，PD表示反射光线，∠CPD＝90°，求∠APC的度数；
2. （2）自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线，a∥b.平面镜AB与BC的夹角∠ABC＝ $\text{[math]}$ ，求 $\text{[math]}$ .
3. （3）如图③，若 $\text{[math]}$ ＝108°，设平面镜CD与BC的夹角∠BCD＝ $\text{[math]}$ （90°＜ $\text{[math]}$ ＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出 $\text{[math]}$ 的度数.（可用含x的代数式表示）.
答案解析收藏纠错 + 选题