① ;②PQ∥AE; ③
;④
;⑤
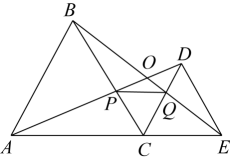


①BC平分∠DCE;②∠ABE+∠ECD=180°;③AC=2BE+CE;④AC=2CD-CE .



①∵ ,
平分
,
∴ , ;
②在中,
的周长为32,
的周长为23,则
的长为 .

已知:在中,
平分
, 且点D是
的中点.求证:
.
方法一:如图2,延长到点E,使
, 连接
.
方法二:如图3,过点D分别作的垂线, 垂足分别为E,F.
例1:“两两分组”:
解:原式
例2:“三一分组”:
解:原式
归纳总结:用分组分解法分解因式要先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
①;
②.
如图1,若 , 射线
在
内郃,
, 求证:
, 小明的做法是:在
上取一点
, 使得
, 再通过已知条件,求得
的度数.请你帮助小明写出证明过程:
如图2,已知 , 当射线
在
内,求
的度数.
如图3,已知 , 当射线
在
下方,
的度数会变化时?若改变,请求出
的度数,若不变,请说明理由.
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形不是等腰三角形
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
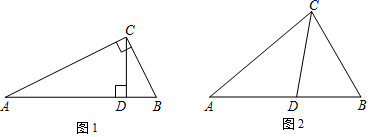
求证:为
的等角分割线.
①如图2,点D在线段上,求证:
;
②点D在线段延长线上,用等式表示线段
和
之间的数量关系,并说明理由.