【培优版】浙教版数学九上3.3 垂径定理同步练习

更新时间：2024-09-10 浏览次数：5 类型：同步测试

一、选择题

1. (2017八下·东营期末) 如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
2. (2024·从江模拟) 如图，AB是 $\text{[math]}$ 的弦，AB的长为6，P是 $\text{[math]}$ 上一个动点(不与点A，B重合).过点O作 $\text{[math]}$ AP于点 $\text{[math]}$ ，作 $\text{[math]}$ 于点 $\text{[math]}$ ，则CD的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2024·凉山州) 数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点A ， B ，连接AB ，作AB的垂直平分线CD交AB于点D ，交 $\text{[math]}$ 于点C ，测出AB＝40cm ， CD＝10cm ，则圆形工件的半径为（　　）

A . 50cm B . 35cm C . 25cm D . 20cm

答案解析收藏纠错 + 选题
4. (2024·乌鲁木齐模拟) 如图，这是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶，其底部是圆球形．球的半径为 $\text{[math]}$ ，瓶内液体的最大深度 $\text{[math]}$ ，则截面圆中弦 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·东莞模拟) 如何只用一张矩形纸条和刻度尺测量出一次性纸杯杯口的直径?小聪同学想到了如下方法：如图所示，将纸条拉直紧贴杯口上，纸条的上下边沿分别与杯口相交于A，B，C，D四点，利用刻度尺量得该纸条宽为3.5cm，AB=3cm，CD=4cm，则纸杯的直径为（）

A . 4cm B . 5cm C . 6cm D . 7cm

答案解析收藏纠错 + 选题
6. (2024·湖南会考) 我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车，如图，筒车盛水桶的运行轨道是以轴心 $\text{[math]}$ 为圆心的圆，已知圆心 $\text{[math]}$ 在水面的上方， $\text{[math]}$ 的半径长为5米， $\text{[math]}$ 被水面截得的弦 $\text{[math]}$ 长为8米，点 $\text{[math]}$ 是运行轨道的最低点，则点 $\text{[math]}$ 到弦 $\text{[math]}$ 的距离为（）

A . 5米 B . 4米 C . 3米 D . 2米

答案解析收藏纠错 + 选题
7. (2024·叙州模拟) 如图，M为弦 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ 过点M作 $\text{[math]}$ 交圆O于点C ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 5 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·自贡) 如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E，若OE＝3，OB＝5，则CD的长度是（）

A . 9.6 B . 4 $\text{[math]}$ C . 5 $\text{[math]}$ D . 10

答案解析收藏纠错 + 选题

二、填空题

9. (2024·牡丹江) 如图，在⊙O中，直径AB⊥CD于点E ， CD＝6，BE＝1，则弦AC的长为．

答案解析收藏纠错 + 选题
10. (2024·修水模拟) “青山绿水，畅享生活”，人们经常将圆柱形竹筒改造成生活用具，图1所示是一个竹筒水容器，图 $\text{[math]}$ 为该竹筒水容器的截面．已知截面的半径为 $\text{[math]}$ ，开口 $\text{[math]}$ 宽为 $\text{[math]}$ ，这个水容器所能装水的最大深度是 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九下·龙湖模拟) 如图，以G（0，3）为圆心，半径为6的圆与x轴交于A ， B两点，与y轴交于C ， D两点，点E为⊙G上一动点，CF⊥AE于F ，点E在G的运动过程中，线段FG的长度的最小值为．

答案解析收藏纠错 + 选题
12. (2024·台州模拟) 如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖 $\text{[math]}$ 与两个磁体组成（下侧磁体固定不动），连接杆EF与地面BD垂直，排水口 $\text{[math]}$ ，密封盖最高点E到地面的距离为6mm，整个地漏的高度EG＝75mm（G为磁体底部中点），密封盖被磁体顶起将排水口密封， $\text{[math]}$ 所在圆的半径为 mm；当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点M'恰好落在BG中点，若点M'到E'F'的距离为36mm，则密封盖下沉的最大距离为 mm．

答案解析收藏纠错 + 选题

三、解答题

13. (2024·南昌模拟)
1. （1）如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）下图是某学校人行过道中的一个以 $\text{[math]}$ 为圆心的圆形拱门，路面 $\text{[math]}$ 的宽为 $\text{[math]}$ ，高 $\text{[math]}$ 为 $\text{[math]}$ ，求圆形拱门所在圆的半径．
答案解析收藏纠错 + 选题
14. (2023九上·吉林期中) 如图①是从正面看到的一个面碗的形状示意图． $\text{[math]}$ 是⊙O的一部分． D是AB的中点，连接OD，与弦AB交于C．连接OA、OB．已知AB=24cm．碗深CD=8cm，问⊙O的半径OA是多少？

答案解析收藏纠错 + 选题
15. 如图，要把破残的圆片复制完整，已知弧上三点A、B、C.
1. （1）用尺规作图法，找出弧BAC所在圆的圆心O；(保留作图痕迹，不写作法)
2. （2）设△ABC为等腰三角形，底边BC=10 cm，腰AB=6 cm，求圆片的半径R；(结果保留根号)
3. （3）若在(2)题中的R满足n＜R＜m(m、n为正整数)，试估算m和n的值.
答案解析收藏纠错 + 选题
16. (2020九上·新建期中) 如图，已知⊙O的弦AB垂直平分半径OC ，连接AO并延长交⊙O于点E ，连接DE ，若AB＝4 $\text{[math]}$ ，请完成下列计算
1. （1）求⊙O的半径长；
2. （2）求DE的长．
答案解析收藏纠错 + 选题

四、实践探究题

17. 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．《九章算术》中记载(如图①)：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”
阅读完这段文字后，聪聪画出了一个圆柱截面示意图(如图②)，其中BO⊥CD于点A，求“间径”就是要求⊙O的直径．根据上面记载的文字，发现AB= 寸，CD= 寸(一尺等于十寸)．运用有关知识即可解决这个问题．请你补全题目条件，并帮助聪聪求出⊙O的直径．

答案解析收藏纠错 + 选题

18. (2023九上·上城期中) 根据背景素材，探索解决问题．

测算石拱桥拱圈的半径
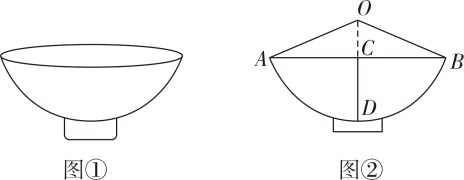
素材1	某数学兴趣小组测算一座石拱桥拱圈的半径（如图1），石拱桥由矩形的花岗岩叠砌而成，上、下的花岗岩错缝连接（花岗岩的各个顶点落在上、下花岗岩各边的中点，如图2所示）．
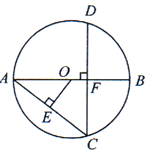
素材2	通过观察发现A，B，C三个点都在拱圈上，A是拱圈的最高点，且在两块花岗岩的连接处，B，C两个点都是花岗岩的顶点（如图3）．
素材3	如果没有带测量工具，那么可以用身体的“尺子”来测，比如前臂长（包括手掌、手指）（如图4），利用该方法测得一块花岗岩的长和宽（如图5）．
问题解决
任务1	获取数据	通过观察、计算B，C两点之间的水平距离及铅垂距离（高度差）．
任务2	分析计算	通过观察、计算石拱桥拱圈的半径．

注：测量、计算时，都以“肘”为单位．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

【培优版】浙教版数学九上3.3 垂径定理同步练习

副标题：

*注意事项：

【培优版】浙教版数学九上3.3 垂径定理同步练习

试题分析

总体分析

题量分析

难度分析

知识点分析

小学

初中

高中

【培优版】浙教版数学九上3.3 垂径定理 同步练习

副标题：

*注意事项：

【培优版】浙教版数学九上3.3 垂径定理 同步练习

试题分析

总体分析

题量分析

难度分析

知识点分析

【培优版】浙教版数学九上3.3 垂径定理同步练习

【培优版】浙教版数学九上3.3 垂径定理同步练习