【提升版】北师大版数学九年级上册6.3反比例函数的应用同步...

更新时间：2024-10-10 浏览次数：2 类型：同步测试

一、选择题

1. (2024九下·二道模拟) 当温度不变时，某气球内的气压 $\text{[math]}$ 与气体体积 $\text{[math]}$ 的函数关系如图所示，已知当气球内的气压 $\text{[math]}$ 时，气球将爆炸，为了安全起见，气球的体积 $\text{[math]}$ 应(　　)

A . 不大于 $\text{[math]}$ B . 大于 $\text{[math]}$ C . 不小于 $\text{[math]}$ D . 小于 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·馆陶期末) 在四个密闭容器中分别装有甲、乙、丙、丁四种气体，如图，用四个点分别描述这四种气体的密度 $\text{[math]}$ 与体积 $\text{[math]}$ 的情况，其中描述乙、丁两种气体情况的点恰好在同一个反比例函数的阁象上，则这四种气体的质量最小的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
3. (2024九上·新宁月考) 某个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图所示的是该台灯的电流 $\text{[math]}$ 与电阻 $\text{[math]}$ 的关系图象，该图象经过点 $\text{[math]}$ ．根据图象可知，下列说法正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ B . I与R的函数表达式是 $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时，则 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·福州月考) 在物理学中，功率表示做功的快慢，功与做功时间的比叫做功率，即所做的功一定时，功率 $\text{[math]}$ 与做功所用的时间 $\text{[math]}$ 成反比例函数关系，图象如图所示，下列说法不正确的是（）

A . P与t的函数关系式为 $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . p随t的增大而减小

答案解析收藏纠错 + 选题
5. (2024·巴东模拟) 已知经过闭合电路的电流 $\text{[math]}$ （单位： $\text{[math]}$ ）与电路的电阻 $\text{[math]}$ （单位： $\text{[math]}$ ）之间的关系如表所示，则下列说法中错误的是（）
$\text{[math]}$
……
5
4
$\text{[math]}$
$\text{[math]}$
2
1
0.5
0.25
……
$\text{[math]}$
……
20
25
30
40
50
100
200
400
……

A . $\text{[math]}$ 的值为2.5 B . $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式为 $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小

答案解析收藏纠错 + 选题
6. (2024九下·邯郸模拟) 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强p（kPa）与汽缸内气体的体积V（mL）成反比例，p关于V的函数图象如图所示．若压强由75kPa加压到100kPa，则气体体积压缩了（　　）

A . 10mL B . 15mL C . 20mL D . 25mL

答案解析收藏纠错 + 选题
7. (2024·南昌模拟) 物理兴趣小组在实验室研究电学时设计了一个电路，其电路图如图1所示．经测试，发现电流I（A）随着电阻R（Ω）的变化而变化，并结合数据描点，连线，画成图2所示的函数图象．若该电路的最小电阻为1Ω，则该电路能通过的（）

A . 最大电流是36A B . 最大电流是27A C . 最小电流是36A D . 最小电流是27A

答案解析收藏纠错 + 选题
8. (2024九上·浦北期末) 某品牌自动饮水机，开机加热时每分钟上升 $\text{[math]}$ ，加热到 $\text{[math]}$ ，停止加热，水温开始下降．此时水温 $\text{[math]}$ 与通电时间 $\text{[math]}$ 成反比例关系．当水温降至 $\text{[math]}$ 时，饮水机再自动加热，若水温在 $\text{[math]}$ 时接通电源，水温 $\text{[math]}$ 与通电时间 $\text{[math]}$ 之间的关系如图所示，则下列说法中正确的是（）

A . 上午 $\text{[math]}$ 点接通电源，可以保证当天 $\text{[math]}$ 能喝到不超过 $\text{[math]}$ 的水 B . 水温下降过程中， $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式是 $\text{[math]}$ C . 水温从 $\text{[math]}$ 加热到 $\text{[math]}$ ，需要 $\text{[math]}$ D . 水温不低于 $\text{[math]}$ 的时间为 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024·江门模拟) 学校科技兴趣小组为探索如图所示的电路中电压 $\text{[math]}$ 、电流 $\text{[math]}$ 、电阻 $\text{[math]}$ 三者之间的关系，测得数据如下，根据数据猜想得到三者之间为： $\text{[math]}$ ．由此可得，当电阻 $\text{[math]}$ 时，电流 $\text{[math]}$ A．
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·惠阳月考) 饮水机中原有水的温度为 $\text{[math]}$ ，通电开机后，饮水机自动开始加热(此过程中，水温 $\text{[math]}$ 与开机时间 $\text{[math]}$ 分满足一次函数关系)，当加热到 $\text{[math]}$ 时自动停止加热，随后水温开始下降(此过程中，水温 $\text{[math]}$ 与开机时间x分成反比例函数关系)，当水温降至 $\text{[math]}$ 时，饮水机又自动开始加热，……如此循环下去(如图所示)．那么开机后 $\text{[math]}$ 分钟时，水的温度是 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九上·雅安期末) 如图，直线 $\text{[math]}$ 与y轴交于点A ，与反比例函数 $\text{[math]}$ 图象交于点C ，过点C作 $\text{[math]}$ 轴于点B ， $\text{[math]}$ ，则k的值为．

答案解析收藏纠错 + 选题
12. (2024九上·松原期末) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ ， $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
13. (2024九上·广水期末) 小明要把一篇文章录入电脑，所需时间y（min）与录入文字的速度x（字/min）之间的函数关系如图所示．如果小明要在7min内完成录入任务，那么他录入文字的速度至少为字/min．

答案解析收藏纠错 + 选题

三、解答题

14. (2024九上·沅江开学考) 如图，一次函数 $\text{[math]}$ 的图象与反比例的数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，与x轴交于点C．
1. （1）求一次函数和反比例函数的表达式；
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
3. （3）直接写出关于x的不等式： $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
15. (2024九上·金沙期末) 如图，在平面直角坐标系中，反比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 两点，直线 $\text{[math]}$ 交y轴于点C ．
1. （1）求反比例函数与一次函数的表达式；
2. （2）直接写出关于x的不等式 $\text{[math]}$ 的解集为．
答案解析收藏纠错 + 选题
16. (2024·金华模拟) 建筑是一门不断演化和创新的艺术，近年来，一种名为双曲铝单板的新兴材料以其独特的曲线和光泽，为建筑注入了新的时尚元素，同时也赋予了建筑更多的创意和流动性．图1为某厂家设计制造的双曲铝单板建筑，其横截面（图2）由两条曲线 $\text{[math]}$ ， $\text{[math]}$ （反比例函数图象的一部分）和若干线段围成，为轴对称图形，其中四边形 $\text{[math]}$ 与四边形 $\text{[math]}$ 均为矩形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以AC的中点 $\text{[math]}$ 为原点， $\text{[math]}$ 所在直线为 $\text{[math]}$ 轴建立平面直角坐标系．

请回答下列问题：
1. （1）如图2，求 $\text{[math]}$ 所在图象的函数表达式．
2. （2）如图3，为在曲面实现自动化操作，工程师安装了支架 $\text{[math]}$ ，并加装了始终垂直于 $\text{[math]}$ 的伸缩机械臂 $\text{[math]}$ 用来雕刻 $\text{[math]}$ 所在曲面的花纹，请问点P在 $\text{[math]}$ 上滑动过程中， $\text{[math]}$ 最长为多少米？
答案解析收藏纠错 + 选题
17. (2024·长沙模拟) 通过实验研究发现：初中生在数学课上听课注意力指标数随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散．学生注意力指标数y随时间x（分）变化的函数图象如图所示．当 $\text{[math]}$ 和 $\text{[math]}$ 时，图象是线段：当 $\text{[math]}$ 时，图象是双曲线的一部分，根据函数图象回答下列问题：
1. （1）点A的注意力指标数是；
2. （2）当 $\text{[math]}$ 时，求注意力指标数y随时间x（分）的函数解析式；
3. （3）张老师在一节课上讲解一道数学综合题需要 $\text{[math]}$ 分钟，他能否经过适当的安排，使学生在听这道综合题的讲解时，注意力指标数都不低于 $\text{[math]}$ ？请说明理由．
答案解析收藏纠错 + 选题
18. (2024九上·松原期末) 驾驶员血液中每毫升的酒精含量大于或等于 $\text{[math]}$ 微克即为酒驾，某研究所经实验测得，成人饮用某品牌 $\text{[math]}$ 度白酒后血液中酒精浓度 $\text{[math]}$ 微克 $\text{[math]}$ 毫升 $\text{[math]}$ 与饮酒时间 $\text{[math]}$ 小时 $\text{[math]}$ 之间函数关系如图所示 $\text{[math]}$ 当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 成反比例 $\text{[math]}$ ．
1. （1）根据图象直接写出：血液中酒精浓度上升阶段的函数解析式为；下降阶段的函数解析式为； $\text{[math]}$ 并写出 $\text{[math]}$ 的取值范围 $\text{[math]}$
2. （2）问血液中酒精浓度不低于 $\text{[math]}$ 微克 $\text{[math]}$ 毫升的持续时间是多少小时？
答案解析收藏纠错 + 选题
19. (2024九上·石家庄期末) 生活中处处充满着趣味数学，如图是河南省某海洋公园娱乐设施“水上滑梯”的侧面图，建立如图坐标系，其中 $\text{[math]}$ 段可以看成是反比例函数 $\text{[math]}$ 图象的一段， $\text{[math]}$ 为水面，矩形 $\text{[math]}$ 为向上攀爬的梯子，每节梯子高 $\text{[math]}$ 米，宽1米．其中点A ， E ， D均在坐标轴上，且 $\text{[math]}$ 轴．
1. （1）求反比例函数的表达式；
2. （2）求出口C点到 $\text{[math]}$ 的距离 $\text{[math]}$ 的长；
3. （3）若滑梯 $\text{[math]}$ 上有一个小球Q ，要求Q到水面的距离不高于3米，则Q到 $\text{[math]}$ 的距离至少是多少米？
答案解析收藏纠错 + 选题
20. 在实验课上，小明做了一个试验．如图，在仪器左边托盘 $\text{[math]}$ (固定)中放置一个物体，在右边托盘 $\text{[math]}$ (可左右移动) 中放置一个可以装水的容器，容器的质量为 $\text{[math]}$ ．在容器中加入一定质量的水，可以使仪器左右平衡．改变托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$ ，记录容器中加入的水的质量，得到下表：
托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$
30
25
20
15
10
容器与水的总质量 $\text{[math]}$
10
12
15
20
30
加入的水的质量 $\text{[math]}$
5
7
10
15
25
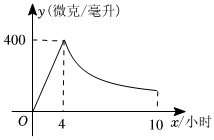
把上表中的 $\text{[math]}$ 与 $\text{[math]}$ 各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图所示的 $\text{[math]}$ 关于 $\text{[math]}$ 的函数图象．
1. （1）请在该平面直角坐标系中作出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数图象．
2. （2）观察函数图象，并结合表中的数据：
  ①猜测 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系，并求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式．
  ②求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式．
  ③当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而 ▲ (填“增大”或“减小”)， $\text{[math]}$ 随 $\text{[math]}$ 的增大而 ▲ (填“增大”或“减小”)， $\text{[math]}$ 的图象可以由 $\text{[math]}$ 的图象向 ▲ (填“上” “下”“左”或“右”)平移得到．
3. （3）若在容器中加入的水的质量 $\text{[math]}$ 满足 $\text{[math]}$ ，求托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

【提升版】北师大版数学九年级上册6.3反比例函数的应用同步...

副标题：

*注意事项：

【提升版】北师大版数学九年级上册6.3反比例函数的应用同步...

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	……	5	4	$\text{[math]}$	$\text{[math]}$	2	1	0.5	0.25	……
$\text{[math]}$	……	20	25	30	40	50	100	200	400	……

托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$	30	25	20	15	10
容器与水的总质量 $\text{[math]}$	10	12	15	20	30
加入的水的质量 $\text{[math]}$	5	7	10	15	25

小学

初中

高中

【提升版】北师大版数学九年级上册6.3反比例函数的应用 同步...

副标题：

*注意事项：

【提升版】北师大版数学九年级上册6.3反比例函数的应用 同步...

试题分析

总体分析

题量分析

难度分析

知识点分析

【提升版】北师大版数学九年级上册6.3反比例函数的应用同步...

【提升版】北师大版数学九年级上册6.3反比例函数的应用同步...