人教版数学九年级全册知识点训练营——辅助圆模型

更新时间：2024-10-10 浏览次数：21 类型：复习试卷

一、定点定长辅助圆

1. (2024九上·深圳开学考) 如图，E、F是正方形 $\text{[math]}$ 边 $\text{[math]}$ 上的两个动点且 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点H．若正方形 $\text{[math]}$ 的边长为2，则线段 $\text{[math]}$ 长度的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·宝安月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，动点E，F分别从点A，C同时出发，以每秒1个单位长度的速度沿 $\text{[math]}$ ， $\text{[math]}$ 向终点B，D运动，过点E，F作直线l，过点A作直线l的垂线，垂足为G，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . 1

答案解析收藏纠错 + 选题
3. (2023九上·湖里月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是矩形 $\text{[math]}$ 内一动点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 面积的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·梁溪期末) 如图，点 $\text{[math]}$ 、 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心 $\text{[math]}$ 为半径作 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 两点，点 $\text{[math]}$ 为 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，取 $\text{[math]}$ 中点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题

二、定角定弦辅助圆

5. (2024九下·剑阁月考) 如图，在菱形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， P是菱形ABCD内或边上的一点，且 $\text{[math]}$ ，连接DP ， CP ，则△DCP的面积的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·惠阳月考) 如图，P为矩形 $\text{[math]}$ 的边 $\text{[math]}$ 的延长线上的动点， $\text{[math]}$ 于H ，点E在边 $\text{[math]}$ 上，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 如图， $\text{[math]}$ O 的半径为6，弦AB=6，点Р为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 9

答案解析收藏纠错 + 选题
8. 如图，在矩形 $\text{[math]}$ 中，已知 $\text{[math]}$ ，现有一根长为 $\text{[math]}$ 的木棒 $\text{[math]}$ 紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则水棒 $\text{[math]}$ 的中点 $\text{[math]}$ 在运动过程中所围成的图形的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图，在等边三角形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 内部的一个动点，且满足 $\text{[math]}$ ，则线段 $\text{[math]}$ 长的最小值为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·淮安月考) 如图，边长为5的菱形 $\text{[math]}$ 的面积为20，E、F分别为边 $\text{[math]}$ 、 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ， $\text{[math]}$ 垂直直线 $\text{[math]}$ 于点G，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
11. (2024九上·海口期末) 如图，已知正方形ABCD的边长为2，E是BC边上的动点，BF⊥AE交CD于点F，垂足为P，连接CP，则CP的最小值为．

答案解析收藏纠错 + 选题
12. 如图， $\text{[math]}$ 分别是正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上的动点，满足 $\text{[math]}$ ，连结 $\text{[math]}$ ，相交于点 $\text{[math]}$ ，连结 $\text{[math]}$ ，若正方形的边长为 2 ，则线段 $\text{[math]}$ 的最小值为

答案解析收藏纠错 + 选题
13. (2024九下·郁南模拟) 如图，Rt△ABC中，∠ACB＝90°，∠CAB＝60°，AB＝4，点P是BC边上的动点，过点C作直AP的垂线，垂足为Q，当点P从点C运动到点B时，点Q的运动路径长为．

答案解析收藏纠错 + 选题
14. 如图，在边长为 6 的等边三角形 $\text{[math]}$ 中， $\text{[math]}$ 分别是边 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ，连结 $\text{[math]}$ 交于点 $\text{[math]}$ ，连结 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为

答案解析收藏纠错 + 选题
15. (2024九上·黄山模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点P是 $\text{[math]}$ 内部的一个动点，连接 $\text{[math]}$ ，且满足 $\text{[math]}$ ，过点P作 $\text{[math]}$ 交 $\text{[math]}$ 于点D．
（1） $\text{[math]}$ ；
（2）当线段 $\text{[math]}$ 最短时， $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
16. (2024·从江模拟) 【问题情境】
在综合实践活动课上，李老师让同桌两位同学用相同的两块含 $\text{[math]}$ 的三角板开展数学探究活动.两块三角板分别记作 $\text{[math]}$ 和 $\text{[math]}$ ，设AB $\text{[math]}$ .
【操作探究】
如图(1)，先将 $\text{[math]}$ 和 $\text{[math]}$ 的边 $\text{[math]}$ 重合，再将 $\text{[math]}$ 绕着点 $\text{[math]}$ 按顺时针方向旋转，旋转角为 $\text{[math]}$ ，旋转过程中 $\text{[math]}$ 保持不动，连接BC.
1. （1）当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ $\text{[math]}$
2. （2）当 $\text{[math]}$ 时，画出图形，并求两块三角板重叠部分图形的面积；
3. （3）如图(2)，取BC的中点 $\text{[math]}$ ，将 $\text{[math]}$ 绕着点 $\text{[math]}$ 旋转一周，点 $\text{[math]}$ 的运动路径长为.
答案解析收藏纠错 + 选题
17. (2024·杭州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以C为圆心， $\text{[math]}$ 为半径作圆.点D为AB上的动点，DP、DQ分别切圆C于点P、点Q，连结PQ，分别交AC和BC于点E、F，取PQ的中点M.
1. （1）当 $\text{[math]}$ 时，求劣弧PQ的度数；
2. （2）当 $\text{[math]}$ 时，求AD的长；
3. （3）连结 $\text{[math]}$ ， $\text{[math]}$ .
  ①证明： $\text{[math]}$ .
  ②在点D的运动过程中，BM是否存在最小值？若存在，直接写出BM的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题

三、定角定高辅助圆

18. 如图，在菱形ABCD中，∠A=60°，AB=6.折叠该菱形，使点A落在边BC上的点M处，折痕分别与边AB，AD相交于点E，F.当点M与点B重合时，EF的长为；当点M的位置变化时，DF长的最大值为.

答案解析收藏纠错 + 选题
19. (2024九下·越秀开学考) 如图所示，ABCD是边长为2的正方形，点E，F分别为边BC，CD上动点（点E不与B，C重合，点F不与C，D重合），且∠EAF＝45°，下列说法：
①点E从B向C运动的过程中，△CEF的周长始终不变；
②以A为圆心，2为半径的圆一定与EF相切；
③△AEF面积有最小值 $\text{[math]}$ ；
④△CEF的面积最大值小于 $\text{[math]}$ ．
其中正确的有 .（填写序号）

答案解析收藏纠错 + 选题
20. (2024九上·南京月考) 【问题提出】
（1）如图1，在四边形ABCD中，AB＝AD，∠BCD＝∠BAD＝90°，AC＝4．求BC+CD的值．
小明提供了他研究这个问题的思路：延长CD至点M，使得DM＝BC，连接AM．可以构造三角形全等，结合勾股定理便可解决这个问题．
【问题解决】
（2）如图2，有一个直径为10cm的圆形配件，现需在该配件上切割出一个四边形孔洞OABC，要求∠O＝60°，∠B＝30°，OA＝OC，求四边形OABC面积的最小值．

答案解析收藏纠错 + 选题

四、最大张角辅助圆

21. (2024九下·温江模拟) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的两个动点，满足 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ． $\text{[math]}$ 的度数为；当 $\text{[math]}$ 最大时，线段 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
22. (2023九上·靖江期末) 如图.在正方形ABCD中，边长为4，M是CD的中点，点P是BC上一个动点，当∠DPM的度数最大时，则BP=.

答案解析收藏纠错 + 选题
23. (2020九上·沭阳期中) 如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点，过点P作PM⊥AB于M，PN⊥CD于N，点Q是MN的中点，当点P沿着圆周从点D逆时针方向运动到点C的过程中，当∠QCN度数取最大值时，线段CQ的长为.

答案解析收藏纠错 + 选题
24. (2023九上·滨海期中) （1）【学习心得】
小赵同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．我们把这个过程称为“化隐圆为显圆”．
①已知：如图1， $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
解：若以点O为圆心、 $\text{[math]}$ 为半径作辅助圆， $\text{[math]}$ 是⊙O的圆心角，而 $\text{[math]}$ 是圆周角，从而可容易得到 $\text{[math]}$ $\text{[math]}$ ．

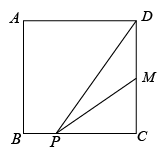
②如图2，点P为正方形 $\text{[math]}$ 内一点，且 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
解：∵ $\text{[math]}$ ， $\text{[math]}$ ， ∴点P在以 $\text{[math]}$ 为直径的圆上
设圆心为点O，则O、P、A三点共线时 $\text{[math]}$ 最小，最小值为______．
（2）【问题解决】
①如图3，在平行四边形 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P是 $\text{[math]}$ 边上一动点（点P不与B，C重合），连接 $\text{[math]}$ ，作点B关于直线 $\text{[math]}$ 的对称点Q，则线段 $\text{[math]}$ 的最小值为______．
②如图4， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于E，求线段 $\text{[math]}$ 的最小值．

（3）【问题拓展】
如图5，在平面直角坐标系中，已知两点 $\text{[math]}$ ， $\text{[math]}$ ， x轴上有一动点P，当 $\text{[math]}$ 最大时，直接写出点P的坐标______．

答案解析收藏纠错 + 选题