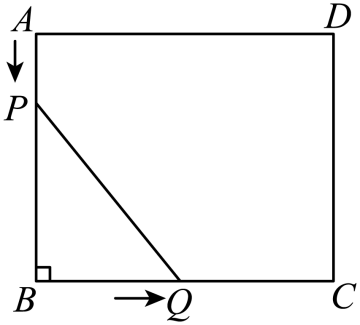
①的长可以为
;
②当农场面积为
时,满足条件的
的长只有一个值;
③农场面积的最大值为
;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过 .
其中,正确结论的是.(只需填序号)


(1)饲养场另一边BC=____米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.

如何利用闲置纸板箱制作储物盒 | ||
素材 | 如图
| |
素材 | 如图是利用闲置纸板箱拆解出的①,②两种均为 | |
长方形纸板① | 长方形纸板② | |
|
| |
小琴分别将长方形纸板①和②以不同的方式制作储物盒. | ||
长方形纸板①的制作方式 | 长方形纸板②制作方式 | |
裁去角上
| 将纸片四个角裁去
| |
目标 | 熟悉材料 | 按照长方形纸板①的制作方式制成的储物盒能够无缝障的放入储物区域,则长方形纸板宽 |
目标 | 利用目标 | |
初步应用 | (1)按照长方形纸板①的制作方式,为了更方便地放入或取出储物盒,盒子四周需要留出一定的空间,当储物盒的底面积是 | |
储物收纳 | (2)按照长方形纸板②的制作方式制作储物盒,若
| |
一元二次方程在几何作图中的应用
如图1,在矩形ABCD中,AB=3,BC=4,求作一个矩形,使其周长和面积分别是矩形ABCD的周长和面积的2倍.

因为矩形ABCD的周长是14,面积是12,所以所求作的矩形周长是28,面积是24
若设所求作的矩形一边的长为x,则与其相邻的一边长为14﹣x,所以,得x(14﹣x)=24,解得x1=2,x2=12
当x=2时,14﹣x=12;当x=12时,14﹣x=2,所以求作的矩形相邻两边长分别是2和12
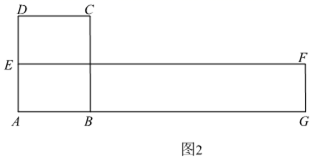
如图2,在边AB的延长线取点G,使得AG=4AB.在AD上取AE= AD,以AG和AE为邻边作出矩形AGFE,则矩形AGFE的周长和面积分别是矩形ABCD的周长和面积的2倍.
学习任务: