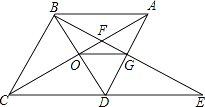
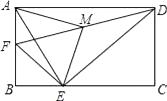
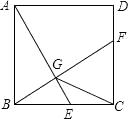
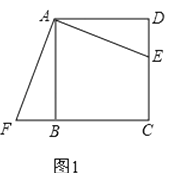
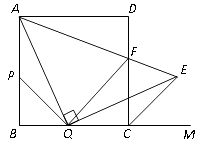
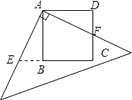
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。若∠ACB=21°,则∠ECD的度数是( )
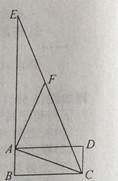


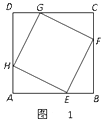
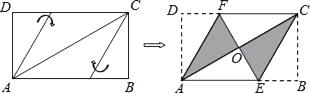
求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
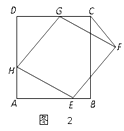
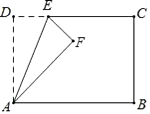
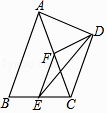
① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由.
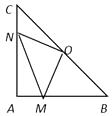
①若点A′落在AB边上,则线段AN的长度为;
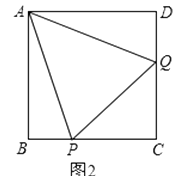
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
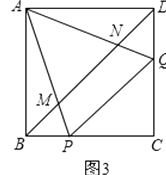
③当点A′落在对角线BD上时,如图4,求 的值.
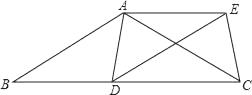
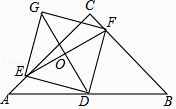
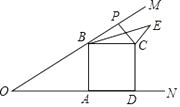
图1中,线段PM与PN的数量关系是,位置关系是;
探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;

把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
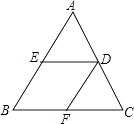
①OG= AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.