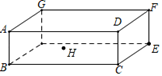
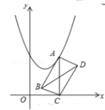
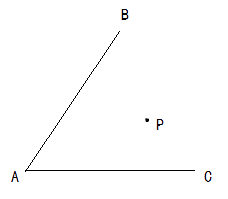
如图,工厂A和工厂B,位于两条公路OC、OD之间的地带,现要建一座货物中转站P.若要求中转站P到两条公路OC、OD的距离相等,且到工厂A和工厂B的距离之和最短,请用尺规作出P的位置.


①如图1,若,请直接写出_▲_;
②如图2,连接p1p2分别交OA、OB于C、D,若,求的度数;
③在②的条件下,若度90<a<180),请直接写出_▲_度(用含a的代数式表示).
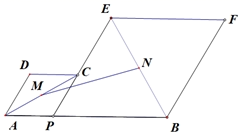
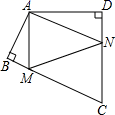
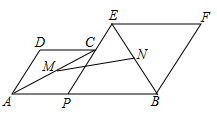
现定义:菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点。
例如:菱形ABCD,P是对角线BD上一点,E、F是边BC和CD上的两点,若点P满足PE与PF之和最小,则称点P为类费马点

①E为BC的中点,F为CD的中点,则PE+PF=。
②E为BC上一动点,F为CD上一动点,且∠ABC=60°则PE+PF=。
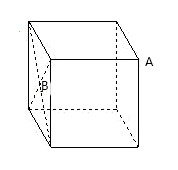
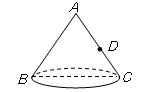
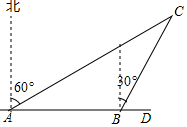
②当∠ABC=30°时,你能找到△ABC的费马点P吗?画图做简要说明,并求此时PA+PB+PC的值
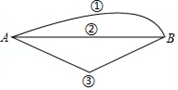
问题:如图1,点A、B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小,小明的思路是:如图2所示,先作点A关于直线l的对称点A',使点A'、B分别位于直线l的两侧,再连接A'B,根据“两点间线段最短”可知A'B与直线l的交点P即为所求.
