 B .
B .  C .
C .  D .
D . 

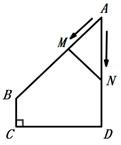
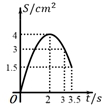 B .
B . 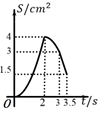 C .
C . 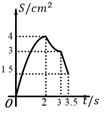 D .
D . 


|
时间 x(天) |
1≤x<50 |
50≤x≤90 |
|
售价(元/件) |
x+40 |
90 |
|
每天销量(件) |
200﹣2x |
|
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.

