浙教版备考2021年中考数学一轮复习专题40 定义新运算

更新时间：2021-05-09 浏览次数：132 类型：一轮复习

一、单选题

1. (2021七上·下城期末) 对于实数 $\text{[math]}$ ， $\text{[math]}$ ，定义运算“ $\text{[math]}$ ”满足： $\text{[math]}$ ．若 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020八下·瑶海期末) 对于实数a、b，定义运算“★”：a★b= $\text{[math]}$ ，关于x的方程（2x+1）★（2x-3）=t恰好有两个不相等的实数根，则t的取值范围是（）

A . t＜ $\text{[math]}$ B . t＞ $\text{[math]}$ C . t＜ $\text{[math]}$ D . t＞ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021七下·永川月考) 定义一种运算“☆”，其规则为 $\text{[math]}$ ，如 $\text{[math]}$ ，根据这个规则计算 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . 13 C . 5 D . 6

答案解析收藏纠错 + 选题
4. (2020七上·宁波期中) 对于任意不相等的两个实数a，b，定义运算：a※b= $\text{[math]}$ +1例如3※2= $\text{[math]}$ =6，那么(-5)※4的值为（）

A . -40 B . -32 C . 18 D . 10

答案解析收藏纠错 + 选题
5. (2021七上·杭州期末) 对于任意非零实数a， b，定义运算“※"如下： "a※b" = $\text{[math]}$ ，则1※2+ 2※3+ 3※4+…+ 2019※2020的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·越城期中) 对于二次函数y=ax²+bx+c(a≠0)，我们把使函数值等于0的实数x叫做这个函数的零点，则二次函数y=x²－mx－5(m为实数)的零点的个数是（）

A . 1 B . 2 C . 0 D . 不能确定

答案解析收藏纠错 + 选题
7. (2024八上·东阳开学考) 任何一个正整数n都可以进行这样的分解：n＝s×t（s，t是正整数，且s≤t），如果p×q在n的所有分解中两因数之差的绝对值最小，我们就称p×q是n的最优分解，并规定：F（n）＝ $\text{[math]}$ .例如24可以分解成1×24，2×12，3×8，4×6这四种，这时就有F（24）＝ $\text{[math]}$ ＝ $\text{[math]}$ .给出下列关于F（n）的说法：①F（6）＝ $\text{[math]}$ ；②F（16）＝1；③F（n²﹣n）＝1﹣ $\text{[math]}$ ；④若n是一个完全平方数，F（n）＝1.其中说法正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2020·温岭模拟) 定义一种新运算 $\text{[math]}$ ＝aⁿ﹣bⁿ ，例如 $\text{[math]}$ ＝k²﹣n² ，若 $\text{[math]}$ ＝﹣ $\text{[math]}$ ，则m为（　　）

A . ﹣1+ $\text{[math]}$ B . ﹣1﹣ $\text{[math]}$ C . $\text{[math]}$ ±1 D . ﹣1± $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九下·湖州月考) 若点M，N分别是两条线段a和b上任意一点，则线段MN长度的最小值叫做线段a与线段b的“理想距离”。已知O（0，0），A（1，1），B（3，k），C（3，k+2），线段BC与线段OA的“理想距离”为2，则k的取值错误的是（）

A . -1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
10. (2020七上·义乌期中) 若“！”是一种数学运算符号，并且1！=1，2！=2×1，3！=3×2×1，且公式 $\text{[math]}$ ，则 $\text{[math]}$ + $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023七上·杭州月考) 对于三个互不相等的有理数a ， b ， c ，我们规定符号 $\text{[math]}$ 表示a ， b ， c三个数中较大的数，例如 $\text{[math]}$ .按照这个规定则方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
12. (2023七上·彭山期中) 对于正整数a、b、c、d，符号 $\text{[math]}$ 表示运算ac-bd，已知1< $\text{[math]}$ <3，则b+d=.

答案解析收藏纠错 + 选题
13. (2021七上·黔南月考) 若规定 $\text{[math]}$ 表示不超过 $\text{[math]}$ 的最大整数，例如 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则在 $\text{[math]}$ 此规定下的值为.

答案解析收藏纠错 + 选题
14. (2020七上·衢州期中) 日常生活中主要运用“十进制”数，而“十六进制”广泛应用于电子技术、计算机编程等领域．十六进制在数学中是一种“逢16进1”的进位制，一般用数字0到9和字母A到F表示，其中用A，B，C，D，E，F分别表示10，11，12，13，14，15．如(2AF5)₁₆表示十六进制数，将它转换成十进制形式是2×16³+10×16²+15×16¹+5×16⁰=10997，那么将十进制数2020转换成十六进制数表示为．

答案解析收藏纠错 + 选题
15. (2019九上·杭州月考) 定义[a ， b ， c]为函数y＝ax²+bx+c的特征数，下面给出特征数为[2m ， 1﹣m ， ﹣1﹣m]的函数的一些结论：
①当m＝﹣1时，函数图象的顶点坐标是（ $\text{[math]}$ ， $\text{[math]}$ ）；

②当m＞0时，函数图象截x轴所得的线段长度大于 $\text{[math]}$ ；

③当m＜0时，函数在 $\text{[math]}$ 时，y随x的增大而减小；

④当m≠0时，函数图象经过x轴上一个定点．

其中正确的结论有．（只需填写序号）

答案解析收藏纠错 + 选题
16. (2020九上·余姚月考) 对于实数a，b定义运算“*”：a*b=a²-ab(a≤b)，a*b=b²-ab(a>b)，关于x的方程(2x-1) * (x-1) =m恰有三个不相等的实数根，则m的取值范围

答案解析收藏纠错 + 选题

三、综合题

17. (2021七下·柯桥月考) 对于有理数 $\text{[math]}$ ，定义一种新的运算“*”： $\text{[math]}$ ，其中 $\text{[math]}$ 为常数，等式右边是通常的加法与乘法运算，已知 $\text{[math]}$ ＝15， $\text{[math]}$ ＝28，求 $\text{[math]}$ 的值

答案解析收藏纠错 + 选题
18. (2020八上·镇海期中) 用[x]表示不大于x的最大整数，如[2.1]=2，[-4.5]=-5，已知x₁ ，x₂是方程6x+7=3[x]的解，且x₁<x₂ ，点A(x₁ ， y₁)和B (x₂ ， y₂)是直线y=-2x-1上的两点，试比较y₁与y₂+l的大小。

答案解析收藏纠错 + 选题
19. (2021七上·温州期末) 如图所示，现有3×3的数阵A，数阵每个位置所对应的数都是1，2或3.定义a*b为数阵中第a行第b列的数.例如：数阵A第3行第2列所对应的数是3，所以3*2=3.
1. （1）对于数阵A，2*3的值为；若2*3=2*x，则x的值为.
2. （2）若一个3×3的数阵对任意的a，b，c均满足以下条件：
  条件一：a*a=a.条件二：（a*b）*c=a*c.
  
  则称此数阵是“有趣的”.
  
  ①请判断数阵A是否是“有趣的”.你的结论：（填“是”或“否”）.
  
  ②已知一个“有趣的”数阵满足1*2=2，试计算2*1的值.
  
  ③是否存在“有趣的”数阵，对任意的a，b满足交换律a*b=b*a?若存在，请写出一个满足条件的数阵；若不存在，请说明理由.
答案解析收藏纠错 + 选题
20. (2019·衢州) 定义：在平面直角坐标系中，对于任意两点A（a，b），B(c，d)，若点T（x，y)满足x= $\text{[math]}$ ，y= $\text{[math]}$ ，那么称点T是点A，B的融合点。
例如：A（-1，8），B（4，-2），当点T（x，y）满是x= $\text{[math]}$ =1，y= $\text{[math]}$ =2时，则点T（1，2）是点A，B的融合点，
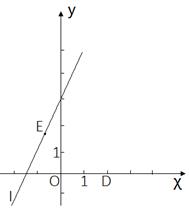
1. （1）已知点A（-1，5），B(7，7)，C（2，4），请说明其中一个点是另外两个点的融合点。
2. （2）如图，点D（3，0），点E（t，2t+3）是直线l上任意一点，点T（x，y)是点D，E的融合点。
  ①试确定y与x的关系式。
  
  ②若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标。
答案解析收藏纠错 + 选题
21. (2021八上·张店期中) 给出如下规定：若实数 $\text{[math]}$ 与 $\text{[math]}$ 的差等于这两个数的积，则称实数对 $\text{[math]}$ 为“关联数”.如实数对 $\text{[math]}$ ，因为 $\text{[math]}$ ， $\text{[math]}$ ，所以实数对 $\text{[math]}$ 是关联数；又如实数对 $\text{[math]}$ 是关联数.
1. （1）若实数对 $\text{[math]}$ 为“关联数”，则 $\text{[math]}$ ， $\text{[math]}$ 应满足的条件用含 $\text{[math]}$ ， $\text{[math]}$ 的等式表示为.
2. （2）判断下列实数对是否是关联数？
  ① $\text{[math]}$ ；
  
  ② $\text{[math]}$ .
3. （3）若实数对 $\text{[math]}$ 是关联数，求 $\text{[math]}$ 的值.
4. （4）是否存在非零实数 $\text{[math]}$ ， $\text{[math]}$ ，使实数对 $\text{[math]}$ 与 $\text{[math]}$ 都是关联数？若存在，求出 $\text{[math]}$ ， $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
22. (2020八上·北仑期末) 定义：在平面直角坐标系中，对于任意两点A(a，b)，B(c，d)，若点T(x，y)满足x= $\text{[math]}$ ，y= $\text{[math]}$ 那么称点T是点A，B的融合点。
例如：A(-1，8)，B(4，-2)，当点T(x，y)满足x= $\text{[math]}$ =1，y= $\text{[math]}$ =2时，则点T(1，2)是点A，B的融合点。
1. （1）已知点A(-1，5)，B(7，7)，C(2，4)，请说明其中一个点是另外两个点的融合点。
2. （2）如图，点D(3，0)，点E(t，2+3)是直线l上任意一点，点T(x，y)是点D，E的融合点。
  ①试确定y与x的关系式。
  
  ②若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标。
答案解析收藏纠错 + 选题
23. (2019九上·南浔月考) 在直角坐标系xOy中，对于点P(x，y) 和Q(x， y′) .给出如下定义：若 $\text{[math]}$ ，则称点Q 为点P 的“可控变点” . 例如：点（1，2）的可控变点为点（1，2），点（-1，3）的可控变点为点（-1，-3）.
1. （1）点（-6，-3）的可控变点坐标为．
2. （2）若点P在函数y＝－x² ＋16的图象上，其可控变点Q的纵坐标y′是7，求可控变点Q的横坐标．
答案解析收藏纠错 + 选题
24. (2020九上·台州月考) 如果关于x的一元二次方程ax²+bx+c=0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为t，则另一个根为2t，因此ax²+bx+c=a(x−t)(x−2t)=ax²−3atx+2t²a，可得；即当时，方程ax²+bx+c=0为倍根方程；下面我们根据此结论来解决问题：
1. （1）方程①x²−x−2=0；方程②x²−6x+8=0这两个方程中，是倍根方程的是(填序号即可)；
2. （2）若(x−2)(mx+n)=0是倍根方程，求4m²+5mn+n²的值；
3. （3）关于x的一元二次方程 $\text{[math]}$ (m⩾0)是倍根方程，且点A(m，n)在一次函数y=3x−8的图象上，求此倍根方程的表达式
答案解析收藏纠错 + 选题
25. (2020八上·玉环期末) 根据同底数幂的乘法法则，我们发现： $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为正整数），类似地我们规定关于任意正整数 $\text{[math]}$ ， $\text{[math]}$ 的一种新运算： $\text{[math]}$ ，请根据这种新运算解决以下问题：
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ ； $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ 的值；
3. （3）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
4. （4）若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
26. (2019九上·天台月考) 对实数a，b定义运算 $\text{[math]}$
1. （1）求函数 $\text{[math]}$ 的解析式；
2. （2）若点 $\text{[math]}$ ， $\text{[math]}$ ( $\text{[math]}$ )在函数 $\text{[math]}$ 的图像上，且A，B两点关于坐标原点成中心对称，求点A的坐标；
3. （3）关于的方程 $\text{[math]}$ 恰有三个互不相等的实数根，则m的取值范围是
答案解析收藏纠错 + 选题